第三章晶格振动与晶体的热学性质

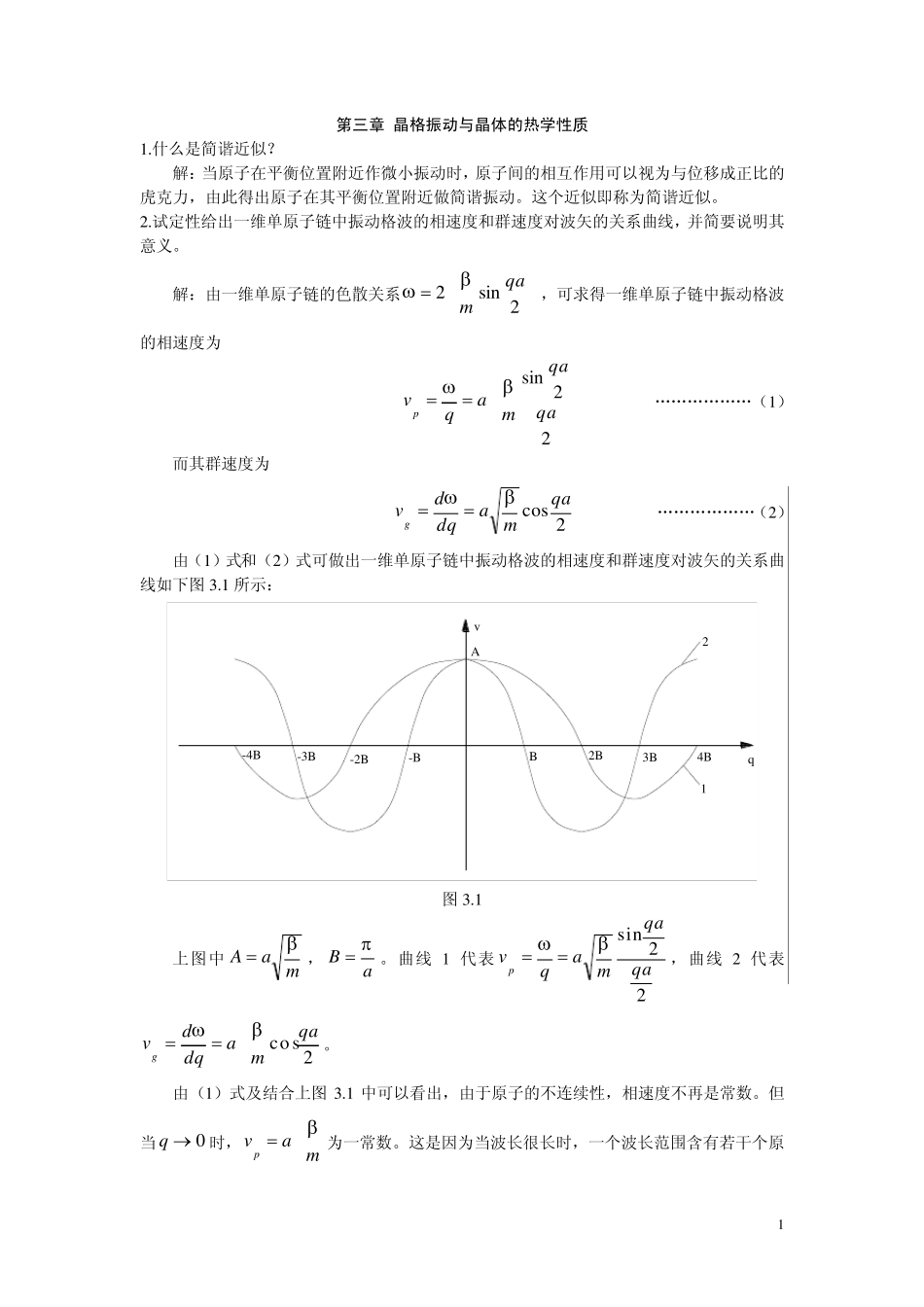
1 第三章 晶格振动与晶体的热学性质 1.什么是简谐近似？ 解：当原子在平衡位置附近作微小振动时，原子间的相互作用可以视为与位移成正比的虎克力，由此得出原子在其平衡位置附近做简谐振动。这个近似即称为简谐近似。 2.试定性给出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线，并简要说明其意义。 解：由一维单原子链的色散关系2sin2qam  ，可求得一维单原子链中振动格波的相速度为 22sinqaqamaqvp  „„„„„„（1） 而其群速度为 2cos qamadqdvg  „„„„„„（2） 由（1）式和（2）式可做出一维单原子链中振动格波的相速度和群速度对波矢的关系曲线如下图 3.1 所示： qv21A-B-2B-3B-4BB2B3B4B 图 3.1 上图中maA，aB。曲线 1 代表22sinqaqamaqvp ，曲线 2 代表2co sqamadqdvg 。 由（1）式及结合上图 3.1 中可以看出，由于原子的不连续性，相速度不再是常数。但当0q时，mavp为一常数。这是因为当波长很长时，一个波长范围含有若干个原 2 子，相邻原子的位相差很小，原子的不连续效应很小，格波接近与连续媒质中的弹性波。 由（2 ）式及结合上图 3 .1 中可以看出，格波的群速度也不等于相速度。但当0q，mavvpg，体现出弹性波的特征，当q 处于第一布区边界上，即aq时，0gv，而mavp2，这表明波矢位于第一布里渊区边界上的格波不能在晶体中传播，实际上它是一种驻波。 3 .周期性边界条件的物理含义是什么？引入这个条件后导致什么结果？如果晶体是无限大，q 的取值将会怎样？ 解：由于实际晶体的大小总是有限的，总存在边界，而显然边界上原子所处的环境与体内原子的不同，从而造成边界处原子的振动状态应该和内部原子有所差别。考虑到边界对内部原子振动状态的影响，波恩和卡门引入了周期性边界条件。其具体含义是设想在一长为Na 的有限晶体边界之外，仍然有无穷多个相同的晶体，并且各块晶体内相对应的原子的运动情况一样，即第 j 个原子和第jtN 个原子的运动情况一样，其中t ＝1 ，2 ，3 „。 引入这个条件后，导致描写晶格振动状态的波矢q 只能取一些分立的不同值。 如果晶体是无限大，波矢 q 的取值将趋于连续。 4 .什么叫声子？对于一给定的晶体，它是否拥有一定种类和一定数目的声子？ 解：声子就是晶格振动中的简谐振子的能量量子，它是一种玻色子，服从玻色－爱因斯坦统计，即具...