第九章应力、应力状态分析(习题解答)

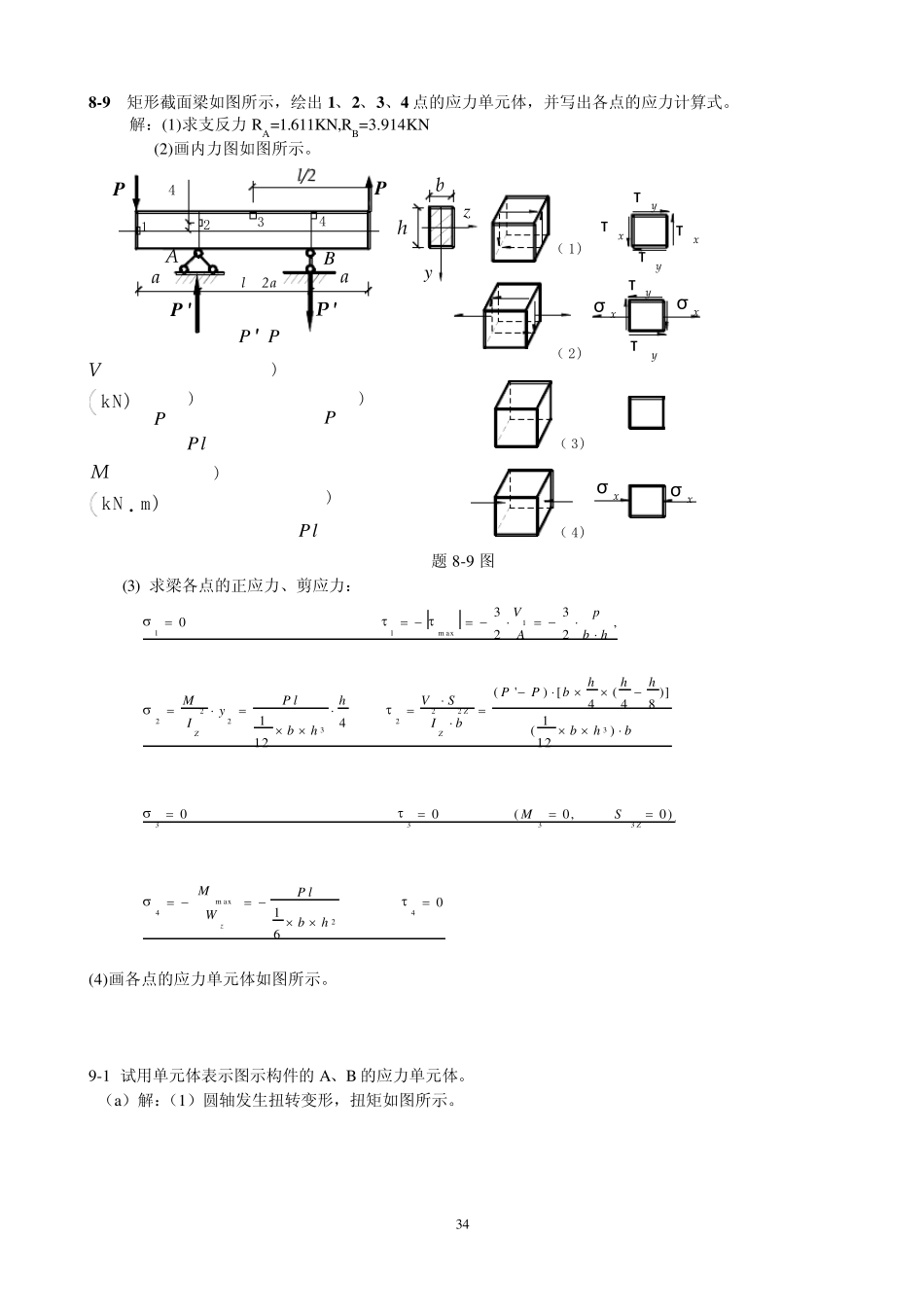
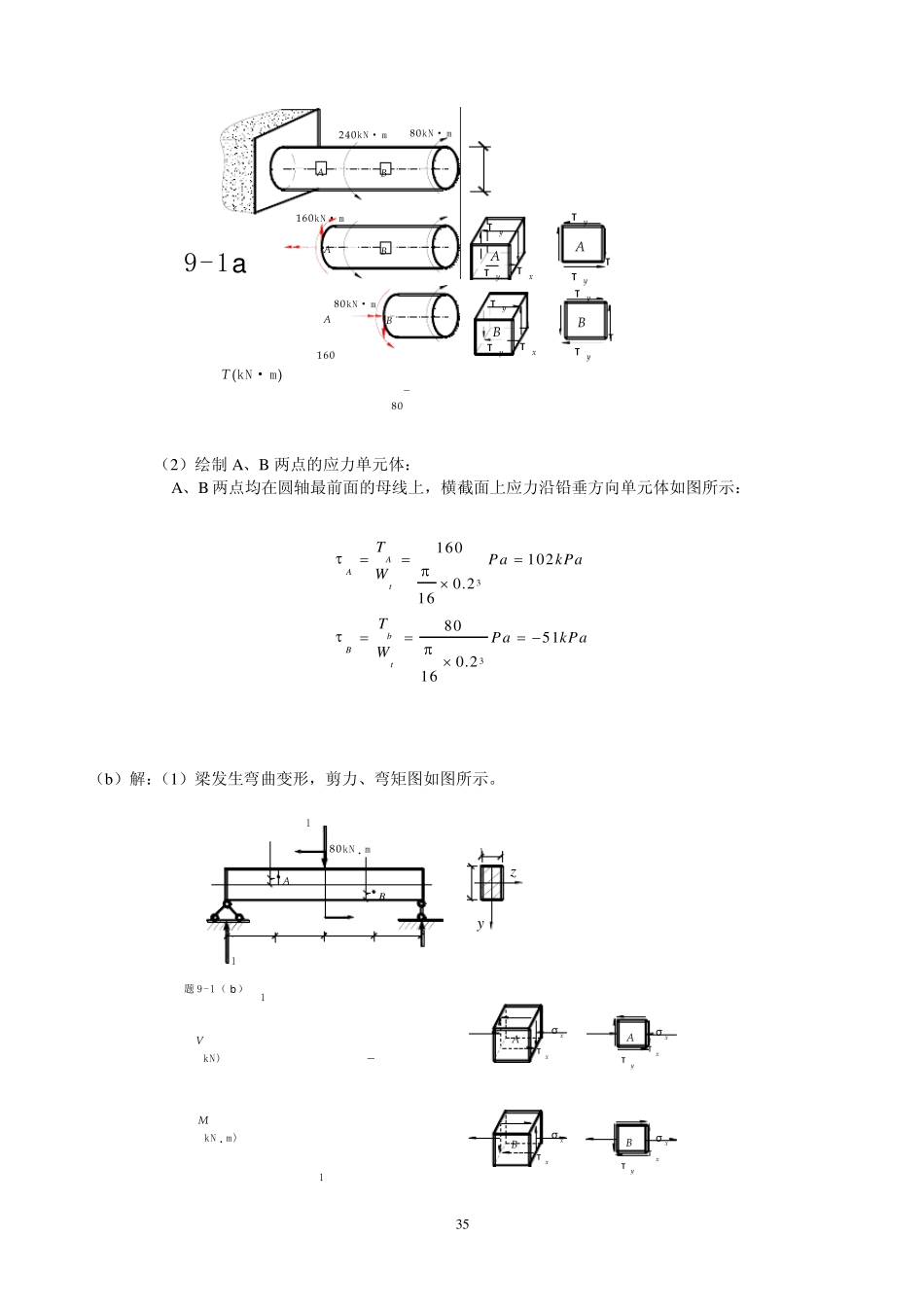
34 8 -9 矩形截面梁如图所示，绘出1、2、3 、4 点的应力单元体，并写出各点的应力计算式。 解：(1)求支反力 RA=1.611KN,RB=3.914KN (2)画内力图如图所示。 xττxPl(-)(+)Plxσxσ（ 4)MkN · m)PPP '-PP 'P 'aal-2aAyττyyτσ xxσBy(-)(-)(+)（ 1)（ 2)（ 3)h/4PbPyzhτ1234VkN) 题 8-9 图 (3) 求梁各点的正应力、剪应力： (4)画各点的应力单元体如图所示。 9-1 试用单元体表示图示构件的 A、B 的应力单元体。 （a）解：（1）圆轴发生扭转变形，扭矩如图所示。 111m ax222222333333m ax442330,22(') [()]448114()121200(0,0)016ZZZZzVpAbhhhhPPbMVSP lhyIIbbhbhbMSMP lWbh      35 9-1aττyAyττyyτxτABτxτyyττyByττ80kN· mBA160kN· mAB-+1608020080kN· m240kN· mAT (kN· m)B （2）绘制A、B 两点的应力单元体： A、B 两点均在圆轴最前面的母线上，横截面上应力沿铅垂方向单元体如图所示： 331601020.21680510.216AAtbBtTPakPaWTPakPaW  （b）解：（1）梁发生弯曲变形，剪力、弯矩图如图所示。 zy160kN0.5m0.5m0.5m0.5m80kN · m5050120kN40kN120200-+120VkN)40MkN · m)+120402060xστ xyτABAAσ xxττ xxστ yxτσ xBB题 9-1（b） 36 （2）绘制A、B 两点的应力单元体： A 点所在截面剪力为正，A 点横截面的剪力为顺时针，同时 A 点所在截弯矩为正下拉，而 A点是压缩区的点。B 点所在截面剪力为负，B 点横截面的剪力为逆时针，同时 B 点所在截弯矩为正下拉，而 B 点是拉伸区的点。单元体如图所示： 333.3333.60100.0537.50.1200.21212010(0.1200.050.075)5.6250.1200.20.1201220100.0512.50.1200.2124010(0.1200.05AAAtAz AAtBBBtBz BBtMyPaM PaIVSPaM PaIbMyPaM PaIVSIb     30.075)1.8750.1200.20.12012PaM Pa  9-2（c）试用解析法求出图示应力单元体 a-a 截面的应力。 30O(M P a)205030aa 解：(1)由题意知： 30,20.5030oxxyM PM PaM P ，，。 (2)求 30o斜截面上的应力 cos2sin 22230503050 cos60( 20)sin 6052.32()223050sin 2cos2sin 60(...