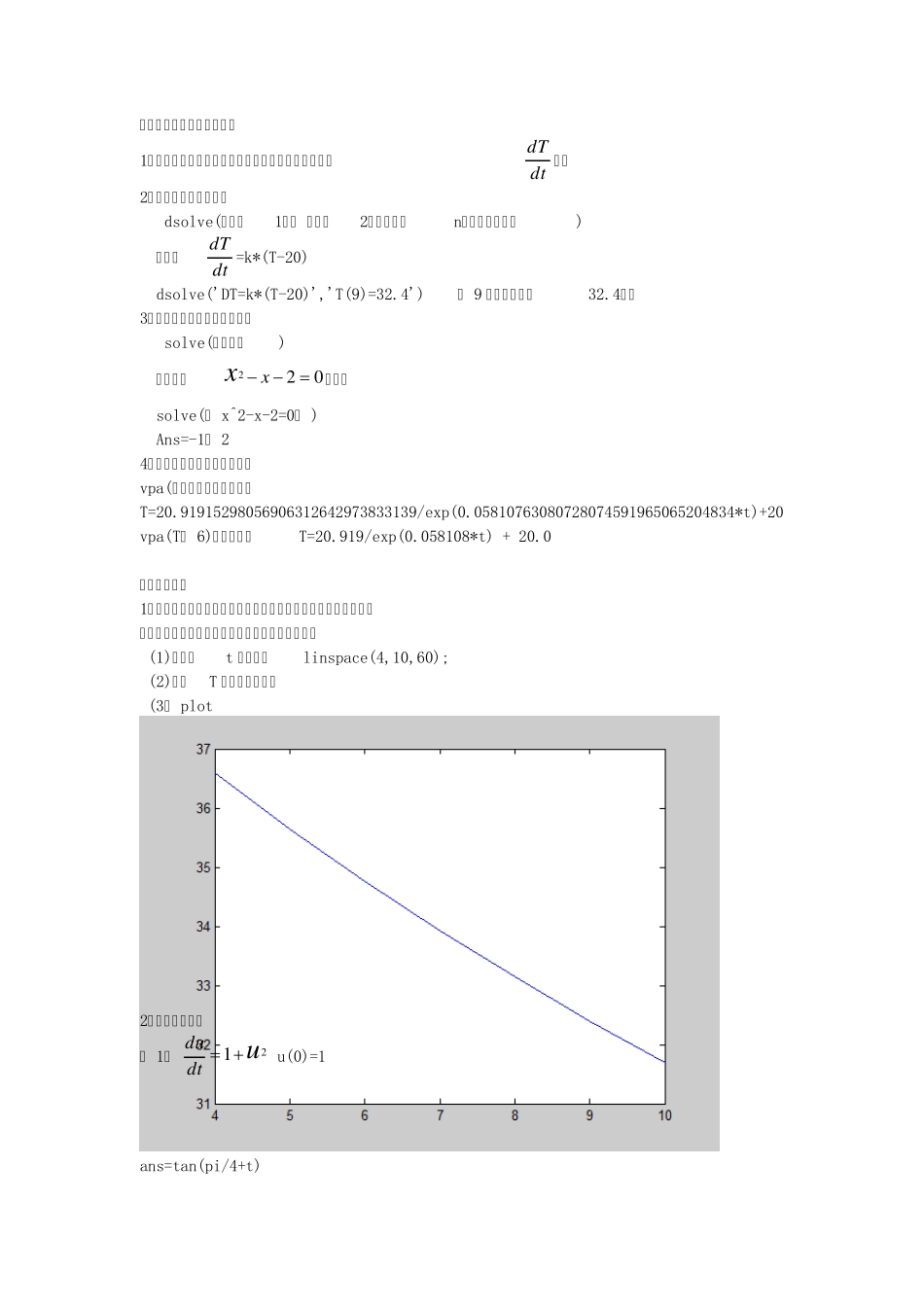
第二讲 导数与微分方程 一、实验内容 1、实际引例 (牛顿冷却模型)警察上午9 点钟发现一被谋杀者,并测得尸体温度为32.4℃,一小时以后,尸体的温度变为31.7℃,尸体所在房间的温度是20℃。如果人的正常体温为36.5℃,并知道热物体冷却速度与自身温度与外界温度之差成正比,试推断谋杀时间。 解 设 T 为尸体温度,t 为时间(十进制,如 10.5 代表10 点 30 分) ,温度的变化率(dtdT)比例常数为K 解题关键热物体冷却速度与自身温度与外界温度之差成正比。 即 dtdT=k*(T-20). 该方程就为微分方程,那么如何求解喃?以下为MATLAB 求解过程: T=dsolve('DT=k*(T-20)','T(9)=32.4') %T( 9)表示在9 点时的温度为32.4℃ ans = (62*exp(k*t))/(5*exp(9*k)) + 20 由于10 点室温为31.7℃,带入后可求K,命令如下: 先输入 solve(''),然后把上面得到的表达式复制进去 (62*exp(k*t))/(5*exp(9*k)) + 20 k=solve('(62*exp(k*10))/(5*exp(9*k)) + 20=31.7') (带入t=10,T=31.7) k=-0.05810763080728074591965065204834 T=(62*exp(k*t))/(5*exp(9*k)) + 20 T=20.91915298056906312642973833139/exp(0.05810763080728074591965065204834*t)+20 T=vpa(T,6) (保留几位数) T =20.9192/exp(0.0581076*t) + 20.0 t=solve('20.9192/exp(0.0581076*t) + 20.0=36.5') ans = 4.0839239039506477826882582186434 0.083923*60=5.0354 即谋杀时间 凌晨4 点 5 分左右 二、引例子所涉及的知识点 1、首先要列出微分方程,简单的来说出现了变化率(dtdT)。 2、如何求解微分方程。 dsolve(‘方程1’, ‘方程2’…‘方程n’’初始条件’) 如求解dtdT=k*(T-20) dsolve('DT=k*(T-20)','T(9)=32.4') ( 9 点时的温度为32.4℃) 3、如何求解方程的未知数的值 solve(‘等式’) 如求解(022 xx)的根 solve(‘ x^2-x-2=0’ ) Ans=-1, 2 4、如何让数据显示指定位数, vpa(函数名,显示的位数) T=20.91915298056906312642973833139/exp(0.05810763080728074591965065204834*t)+20 vpa(T, 6),显示结果T=20.919/exp(0.058108*t) + 20.0 三、过手练习 1、理解以后自己从头来解决引例。最后画出该过程的函数图像。 (提示)画图时,请重新手打以下内容,切勿复制 (1)先要给t 定义域,linspace(4,10,60); (2)写出T 的函数关系式。 (3) plot 2、微分方程求解 ( 1)udtdu21...