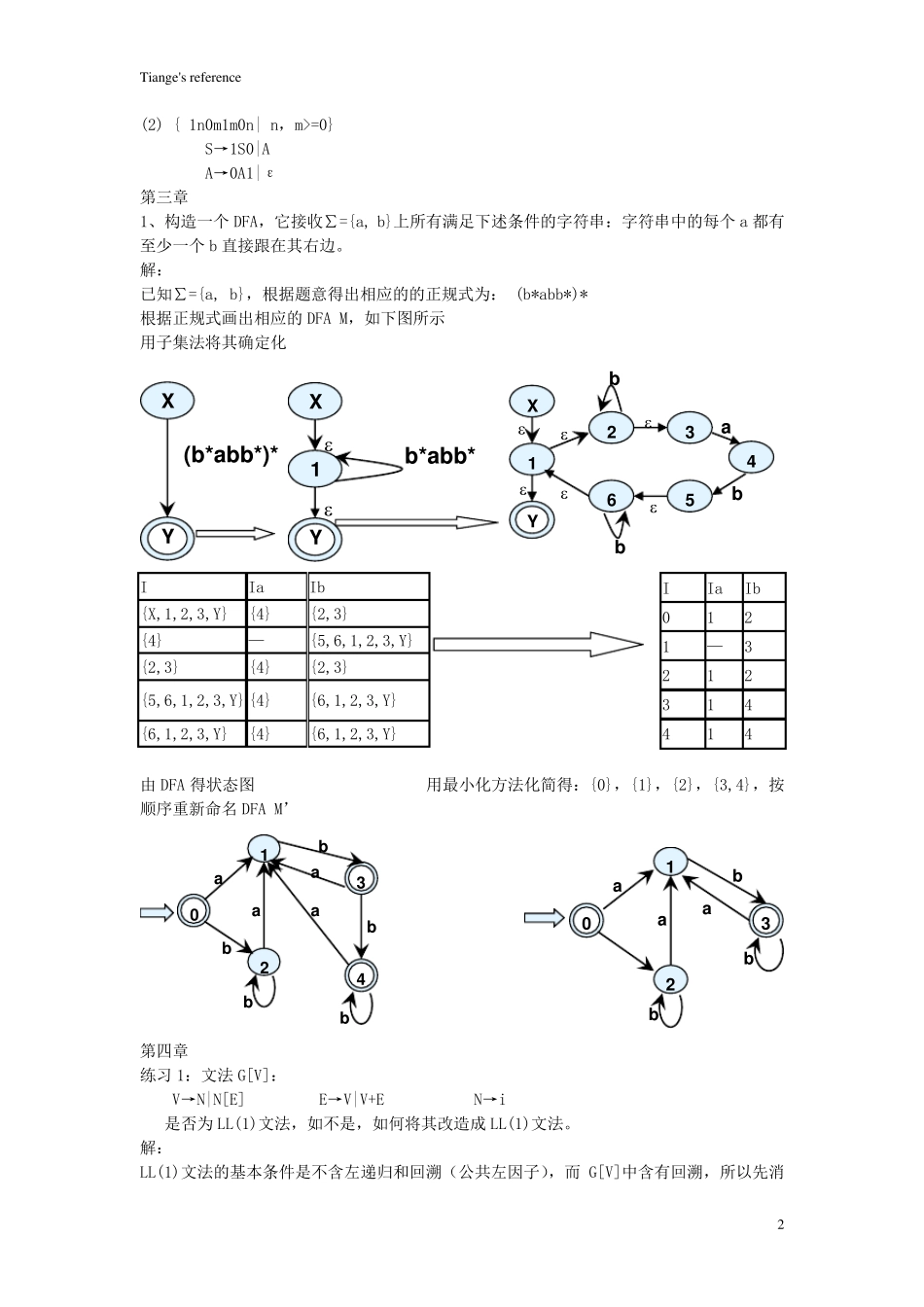
Tiange's reference 1 第一章 ▪ 什么是编译器? ▪ 编译程序的结构分为几个阶段,各阶段的任务是什么? ▪ 遍、编译前端及编译后端的含义? ▪ 编译程序的生成方式有哪些? 第二章 ▪ 1. 写一文法,使其语言是偶正整数的集合。 ▪ 要求:(1)允许0 打头 (2) 不允许0 打头 解:(1)允许0 开头的偶正整数集合的文法 E→NT|D T→NT|D N→D|1|3|5|7|9 D→0|2|4|6|8 (2)不允许0 开头的偶正整数集合的文法 E→NT|D T→FT|G N→D|1|3|5|7|9 D→2|4|6|8 F→N|0 G→D|0 2.证明下述文法G[〈表达式〉]是二义的。 〈表达式〉∷=a|(〈表达式〉)|〈表达式〉〈运算符〉〈表达式〉 〈运算符〉∷=+|-|*|/ 解:可为句子a+a*a 构造两个不同的最右推导: 最右推导1 〈表达式〉〈表达式〉〈运算符〉〈表达式〉 〈表达式〉〈运算符〉a 〈表达式〉* a 〈表达式〉〈运算符〉〈表达式〉* a 〈表达式〉〈运算符〉a * a 〈表达式〉+ a * a a + a * a 最右推导2 〈表达式〉〈表达式〉〈运算符〉〈表达式〉 〈表达式〉〈运算符〉〈表达式〉〈运算符〉〈表达式〉 〈表达式〉〈运算符〉〈表达式〉〈运算符〉 a 〈表达式〉〈运算符〉〈表达式〉 * a 〈表达式〉〈运算符〉a * a 〈表达式〉+ a * a a + a * a 3. 给出生成下述语言的上下文无关文法: (1){ anbnambm| n,m>=0} (2){ 1n0m1m0n| n,m>=0} 解: (1){ anbnambm| n,m>=0} S→AA A→aAb|ε Tiange's reference 2 (2) { 1n0m1m0n| n,m>=0} S→1S0|A A→0A1|ε 第三章 1、构造一个 DFA,它接收∑={a, b}上所有满足下述条件的字符串:字符串中的每个 a 都有至少一个 b 直接跟在其右边。 解: 已知∑={a, b},根据题意得出相应的的正规式为: (b*abb*)* 根据正规式画出相应的 DFA M,如下图所示 用子集法将其确定化 I Ia Ib {X,1,2,3,Y} {4} {2,3} {4} — {5,6,1,2,3,Y} {2,3} {4} {2,3} {5,6,1,2,3,Y} {4} {6,1,2,3,Y} {6,1,2,3,Y} {4} {6,1,2,3,Y} 由 DFA 得状态图 用最小化方法化简得:{0},{1},{2},{3,4},按顺序重新命名 DFA M’ 第四章 练习 1:文法 G[V]: V→N|N[E] E→V|V+E N→i 是否为 LL(1)文法,如不是,如何将其改造成 LL(1)文法。 解: LL(1)文法的基本条件是不含左递归和回溯(公共左因子...