2优化设计的数学基础

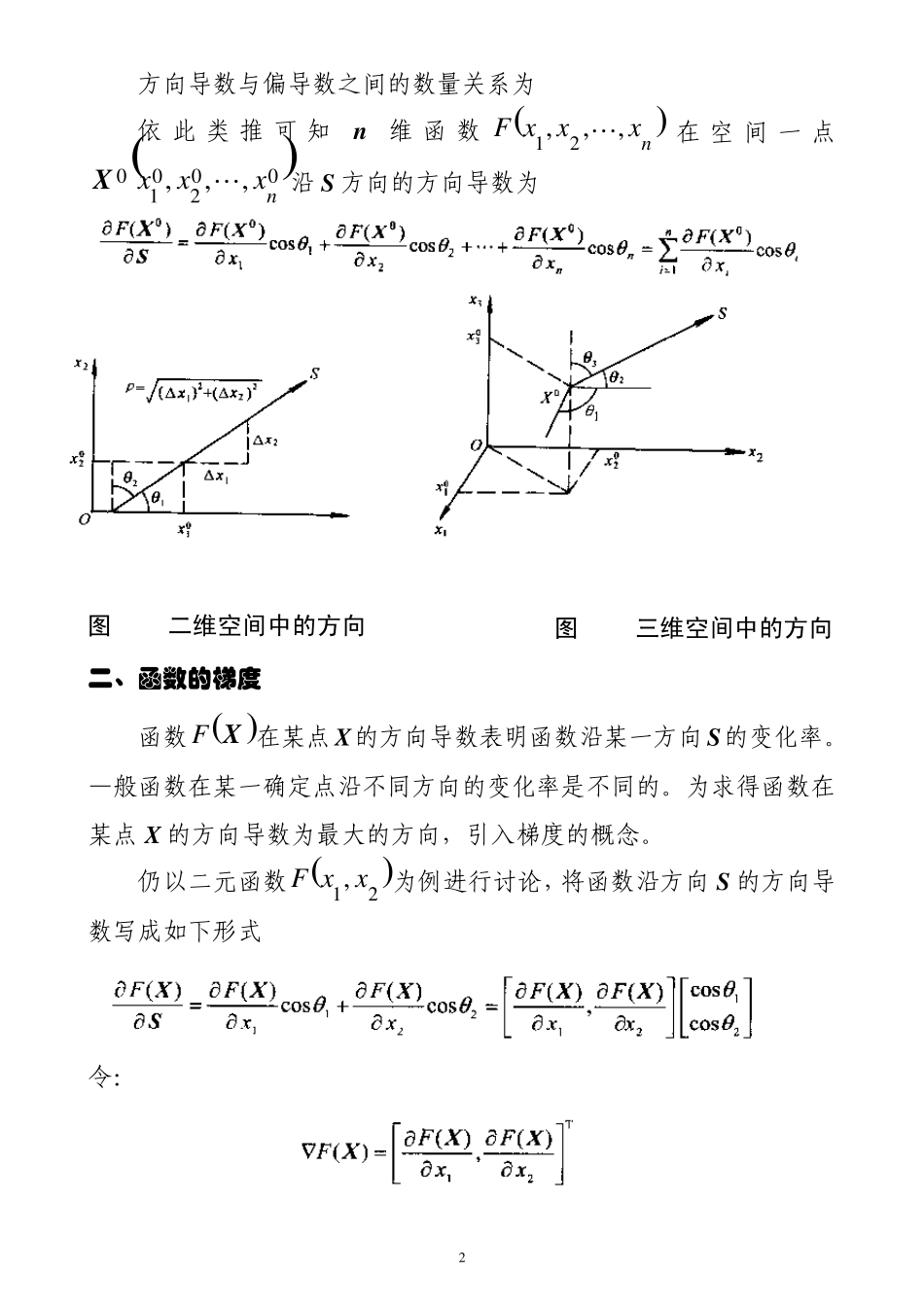
1 第二章 优化设计的数学基础 优化设计中绝大多数是多变量有约束的非线性规划问题，即是求解多变量非线性函数的极值问题。由此可见，优化设计是建立在多元函数的极值理论基础上的，对于无约束优化问题为数学上的无条件极值问题，而对于约束优化问题则为数学上的条件极值问题。本章主要叙述与此相关的数学基础知识。 第一节 函数的方向导数与梯度 一、函数的方向导数 一个二元函数21 , xxF在点02010, xxX处的偏导数，即函数沿坐标轴方向的变化率定义为： 而沿空间任一方向 S 的变化率即方向导数为： 2 方向导数与偏导数之间的数量关系为 依此类推可知n 维函数nxxxF,,,21在空间一点002010,,,nxxxX沿S 方向的方向导数为 二、函数的梯度 函数 XF在某点X的方向导数表明函数沿某一方向S的变化率。—般函数在某一确定点沿不同方向的变化率是不同的。为求得函数在某点X 的方向导数为最大的方向，引入梯度的概念。 仍以二元函数21 , xxF为例进行讨论，将函数沿方向S 的方向导数写成如下形式 令： 图2-1 二维空间中的方向 图2-2 三维空间中的方向 3 称为21, xxF在点X 处的梯度 XFgrad，而同时设S 为单位向量 于是方向导数可写为： 此式表明，函数 XF沿S 方向的方向导数等于向量 XF在S方向上的投影。且当  1,cosSXF，即向量 XF与 S 的方向相向时，向量 XF在S 方向上的投影最大，其值为 XF。这表明梯度 XF是函数 XF在点X 处方向导数最大的方向，也就是导数变化率最大的方向。 上述梯度的定义和运算可以推广到 n维函数中去，即对于n元函数nxxxF,,,21，其梯度定义为 由此可见，梯度是一个向量，梯度方向是函数具有最大变化率的方向。即梯度 XF方向是函数 XF的最速上升方向，而负梯度 XF方向则为函数 XF的最速下降方向。 例2-1 求 二 元 函数 2214xxFX在  T1,10 X点沿44211S和63212S的方向导数。 解：   21212142xxxxFxFFXXX，将 T1,10 X代入可得 4  42XF，因此 而 这说明同一函数在不同方向上的方向导数不同，其变化率也不同。函数 XF由0X 出发，沿S1 方向的变...