ARDL模型的运用实验指导

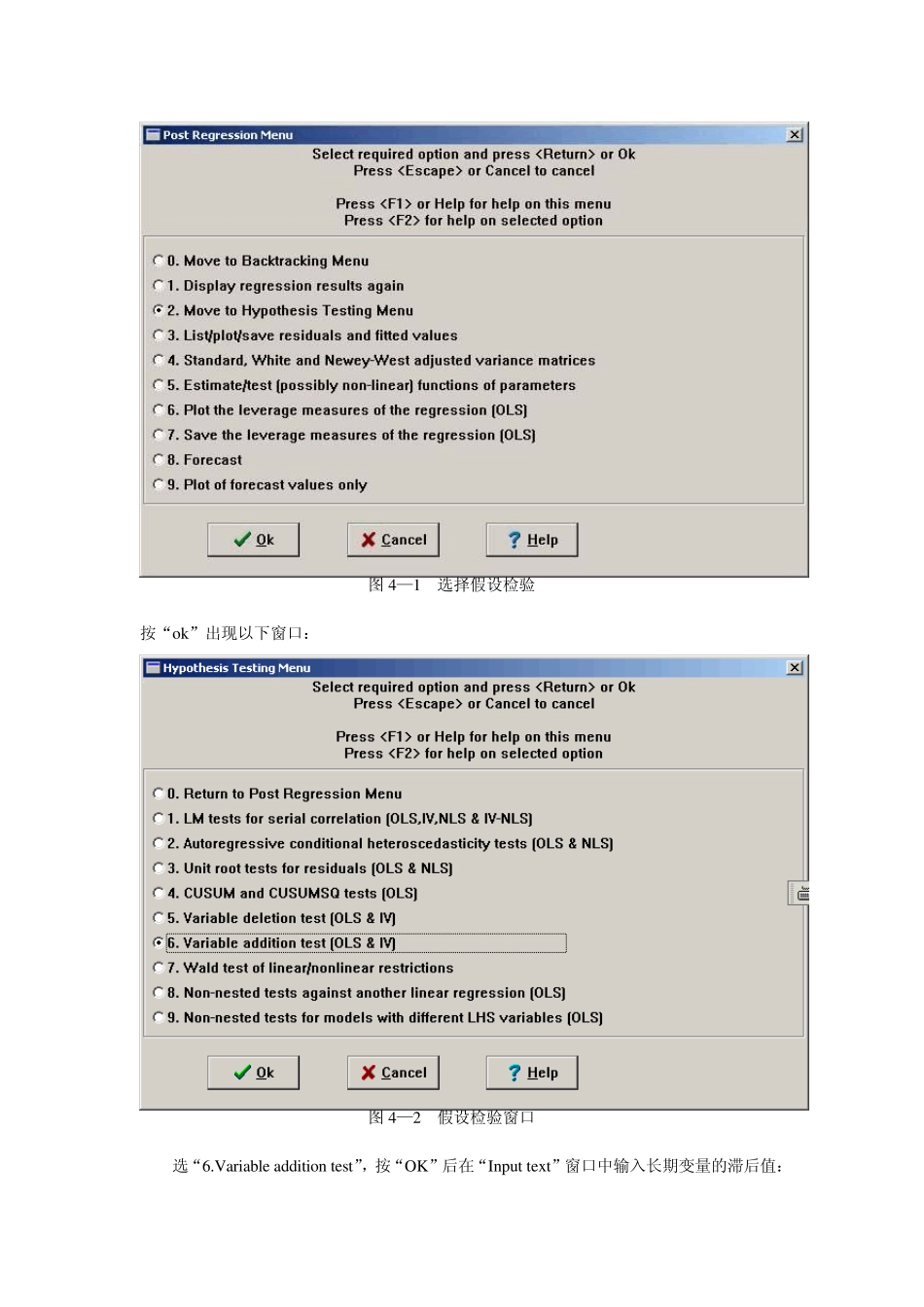
ARDL 模型的运用实验指导 一、实验目的： 理解ARDL 模型的原理与应用条件，运用ARDL 模型，估计变量之间长期关系的系数。注意，只有当能够确定第一步所估计的变量间的长期关系是肯定存在的，而不是伪回归，那么才能应用该模型进行估计。 二、基本概念： ARDL(autoregressive distributed lag)称为自回归分布滞后模型。ARDL 模型的一大优点，就是我们不用管变量是否同为 过程，或同为 过程，都可以用ARDL 模型来检验变量之间的长期关系，而这是标准的协整检验所做不到的。 三、实验内容及要求： 运用ARDL 模型研究美国非耐用消费品支出LC(取对数形式)与真实可支配收入LY(取对数形式)，通胀率PI 之间的关系，数据为1960 年 1 季度到1994 年 1 季度的季度数据。 要求：在认真理解本章内容的基础上，通过实验掌握ARDL 模型的实际应用方法，并熟悉Microfit 软件的基本使用方法。 四、实验指导： ARDL 模型的主要优点在于不管回归项是(0)I还是(1)I，都可以进行检验和估计。而进行标准的协整分析前，必须把变量分类成(0)I和(1)I。 首先，我们调用Microfit 软件读入EX6.1 的数据文件。对原始数据进行取对数作差分的处理。 由于观测值是季度数据，ARDL 模型中最大滞后阶数取4 阶， 利用1960 年 1 季度到1992年 4 季度的样本区间进行估计，1993 年 1 季度到1994 年 1 季度的数据进行预测。 对应于ARDL(4,4,4)中变量LC， LY 和 DP 的误差修正模型（ECM）如下： 4440111112131 tit iit iit iiiittttDLCab DLCd DLYe DPILCLYPIu （ 6.4） 检验的原假设是：变量间不存在稳定的长期关系。 即：0123:0H 备择假设是：11:0H 或20 或30  检验123,,   联合显著的统计量就是我们熟悉的F 统计量。为了计算F 统计量，在Microfit 中选择Single，在编辑窗中输入： DLC INPT DLC{1-4} DLY{1-4} DPI{1-4} 选择估计样本期1960 年 1 季度到1992 年 4 季度，按 START， 然后按OK， 就得到了用OLS 估计的一阶差分的回归结果，这个结果对我们没有直接的用途。按 CLOSE 回到选择菜单，选“2.Move to hypothesis testing menu”，如图。 图4—1 选择假设检验 按“ok”出现以下窗口： 图4—2 假设检验窗口 选“6.Variable addition test”，按“OK”后在“Inpu t tex t”窗口中输入长期变...