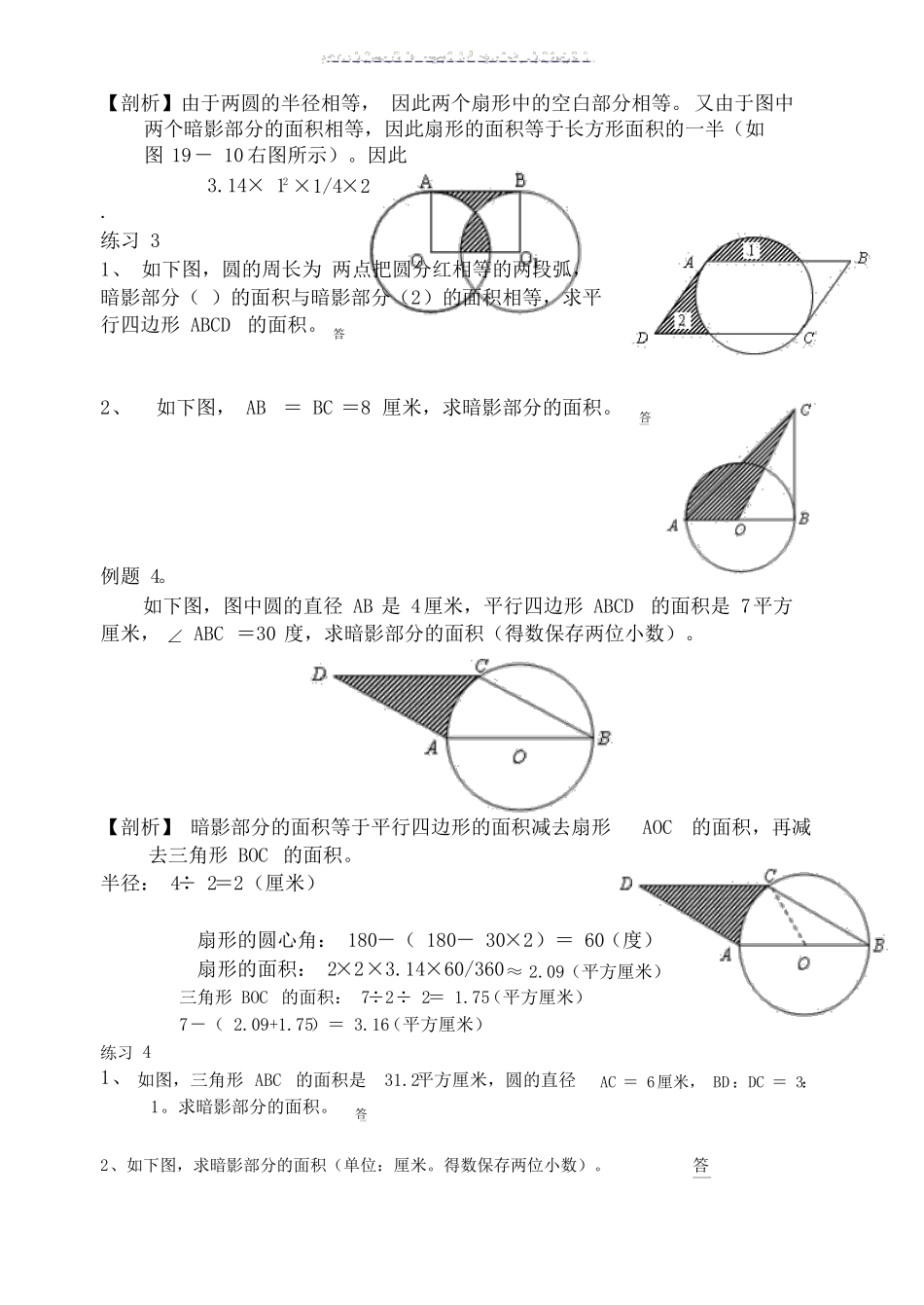
平面图形面积————圆的面积专题简析 :在进行组合图形的面积计算时,要认真察看,认真思虑,看清组合图形是由几个基本单位构成的, 还要找出图中的隐蔽条件与已知条件和要求的问题间的关系。而且同学们应当切记几个常有的圆与正方形的关系量: 在正方形里的3.14 ,而在圆内的最大正方形占所在圆最大圆的面积占所在正方形的面积的42的面积的 3.14 ,这些知识点都应当常记于心,并紧紧掌握!.例题 1。求图中暗影部分的面积(单位:厘米)。【剖析】 如下图的特色,暗影部分的面积能够拼成1/4 圆的面积。62 ×3.14× 1/4= 28.26(平方厘米).练习 11.求下边各个图形中暗影部分的面积(单位:厘米)。2.求下边各个图形中暗影部分的面积(单位:厘米)。答例题 2。求图中暗影部分的面积(单位:厘米)。【剖析】 暗影部分经过翻折挪动地点后,构成了一个新的图形(如下图)。从图中能够看出暗影部分的面积等于大扇形的面积减去大三角形面积的一半。3.14× 42 ×1/4-4×4÷2÷2=8.56(平方厘米)练习 21、计算下边图形中暗影部分的面积(单位:厘米,正方形边长4)。 答2、计算下边图形中暗影部分的面积(单位:厘米,正方形边长4)。 答12. 1 11例题 3。如图 19-10 所示,两圆半径都是 1厘米,且图中两个暗影部分的面积相等。求长方形 ABO1O 的面积。【剖析】由于两圆的半径相等, 因此两个扇形中的空白部分相等。又由于图中两个暗影部分的面积相等,因此扇形的面积等于长方形面积的一半(如图 19- 10 右图所示)。因此23.14× 1 ×1/4×2.练习 31、 如下图,圆的周长为 两点把圆分红相等的两段弧,暗影部分( )的面积与暗影部分(2)的面积相等,求平行四边形 ABCD的面积。 答2、如下图, AB= BC =8 厘米,求暗影部分的面积。答例题 4。如下图,图中圆的直径 AB 是 4厘米,平行四边形 ABCD的面积是 7平方厘米, ∠ ABC =30 度,求暗影部分的面积(得数保存两位小数)。【剖析】 暗影部分的面积等于平行四边形的面积减去扇形去三角形 BOC 的面积。半径: 4÷ 2=2(厘米)AOC的面积,再减扇形的圆心角: 180-( 180- 30×2)= 60(度)扇形的面积: 2×2×3.14×60/360≈ 2.09(平方厘米)三角形 BOC 的面积: 7÷2÷ 2= 1.75(平方厘米)7-( 2.09+1.75)= 3.16(平方厘米)练习 41、 如图,三角形 ABC 的面积是 31.2平方厘米,圆的直径1。求暗影部分的...