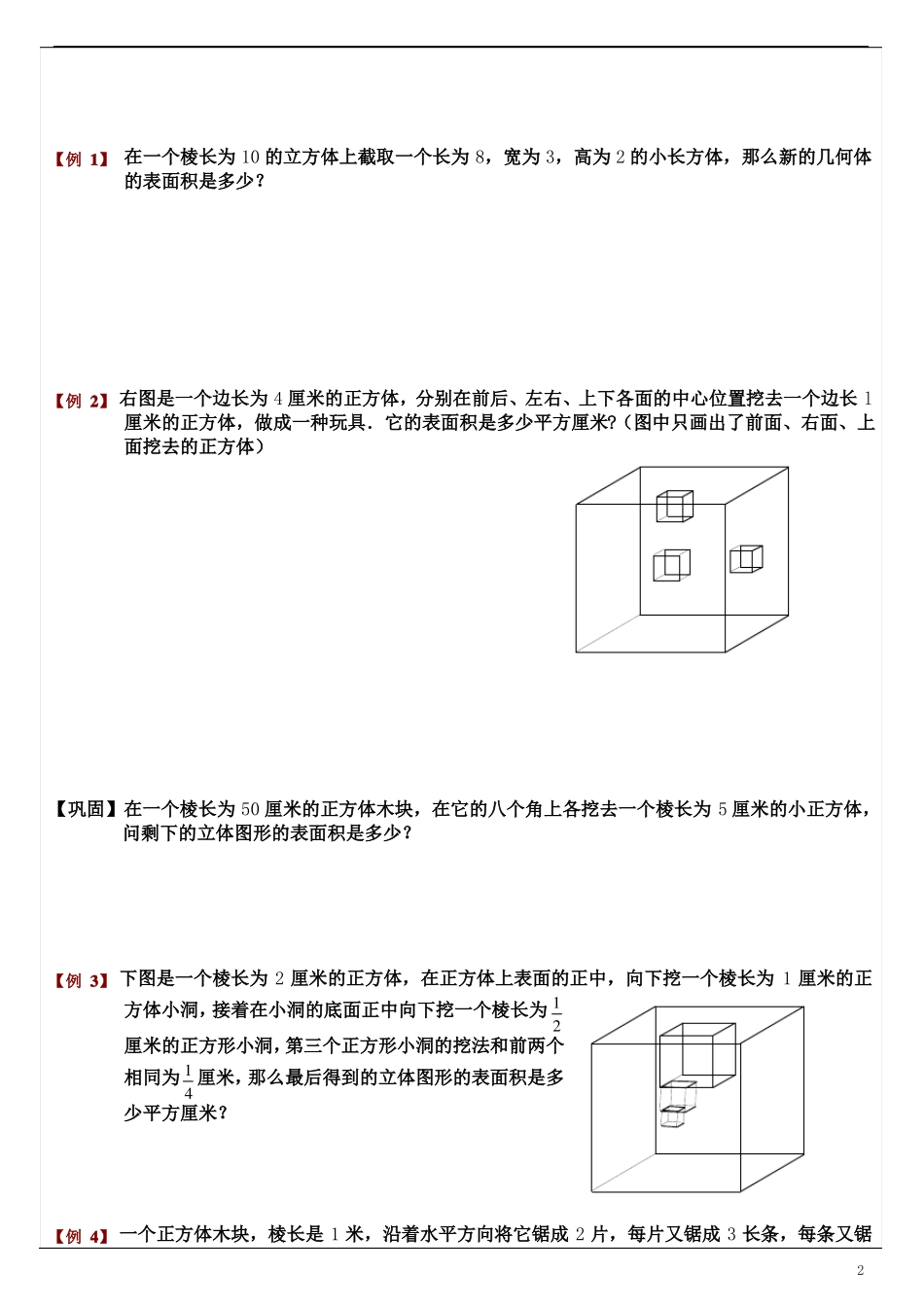
立体部分 ---表面积与体积教学目的 1,掌握空间图形的变面积以及体积的求法。2,加强练习,熟练方法。教学内容知识点对于小学几何而言,立体图形的表面积和体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试都很重视对立体图形的考查.知识点拨:一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.HEDaFCcBbGA①在六个面中,两个对面是全等的,即三组对面两两全等.(叠放在一起能够完全重合的两个图形称为全等图形.)②长方体的表面积和体积的计算公式是:长方体的表面积: S长方体 2(ab bc ca) ;长方体的体积:V长方体 abc.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形.如果它的棱长为 a ,那么: S正方体 6a2 ,V正方体 a3.二、圆柱与圆锥立体图形h表面积S圆柱 侧面积 2个底面积 2πrh 2πr2体积V圆柱 πr2h圆柱rrS圆锥 侧面积 底面积 n πl2 πr23601V圆锥体 πr2h3h圆锥注: l 是母线,即从顶点到底面圆上的线段长例题与巩固1【例 1】 在一个棱长为 10 的立方体上截取一个长为 8,宽为 3,高为 2 的小长方体,那么新的几何体的表面积是多少?【例 2】 右图是一个边长为 4 厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长 l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【巩固】在一个棱长为 50 厘米的正方体木块,在它的八个角上各挖去一个棱长为 5 厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】 下图是一个棱长为 2 厘米的正方体,在正方体上表面的正中,向下挖一个棱长为 1 厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1412厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】 一个正方体木块,棱长是 1 米,沿着水平方向将它锯成 2 片,每片又锯成 3 长条,每条又锯2成 4 小块,共得到大大小小的长方体 24 块,那么这 24 块长方体的表面积之和是多少?【巩固】一个表面积为 56cm 2的长方体如图切成27 个小长方体,这27 个小长方体表面积的和是cm 2 .【例 5】 如图,25 块边长为 1 的正方...