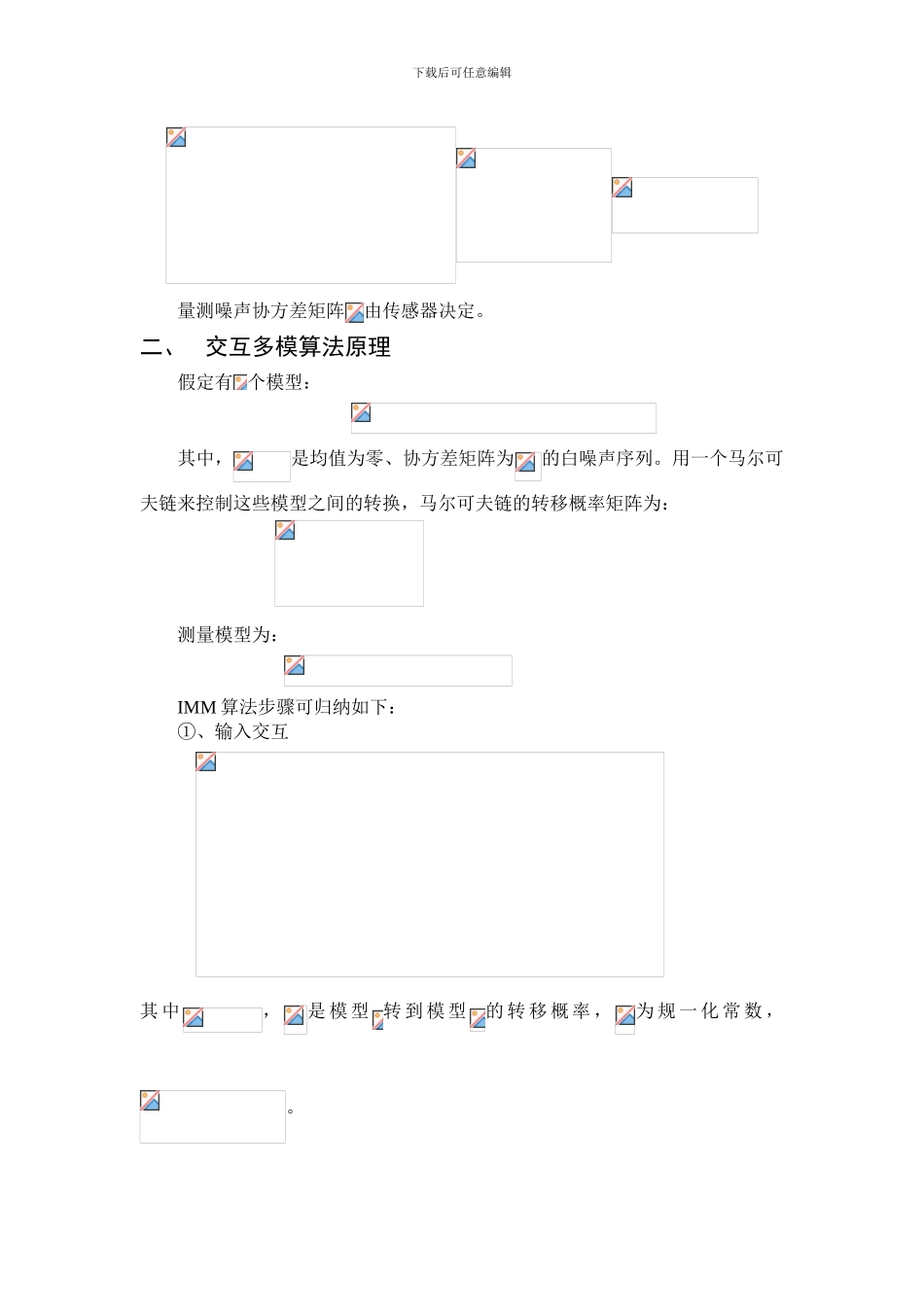
下载后可任意编辑基于交互式多模型方法的目标跟踪高海南 3110038011一、目标建模我们设定一个目标在二维平面内运动,其状态由位置、速度和加速度组成,即。假设采样间隔为,目标检测概率,无虚警存在,在笛卡尔坐标系下目标的离散运动模型和观测模型 (假定在采样时刻)为:目标在二维平面内运动模型如下:1.CV:近似匀速运动模型CV 模 型 将 加 速 度 看 作 是 随 机 扰 动 ( 状 态 噪 声 ) , 取 目 标 状 态。则状态转移矩阵,干扰转移矩阵和观测矩阵分别为:,2.CT:匀速转弯模型只考虑运动角速度已知的 CT 模型。则状态转移矩阵,干扰转移矩阵和观测矩阵分别为:下载后可任意编辑量测噪声协方差矩阵由传感器决定。二、交互多模算法原理假定有 个模型: 其中,是均值为零、协方差矩阵为的白噪声序列。用一个马尔可夫链来控制这些模型之间的转换,马尔可夫链的转移概率矩阵为: 测量模型为: IMM 算法步骤可归纳如下:①、输入交互 其 中,是 模 型 转 到 模 型的 转 移 概 率 ,为 规 一 化 常 数 ,。下载后可任意编辑②、对应于模型,以,及作为输入进行 Kalman 滤波。1)预测 2)预测误差方差阵 3)卡尔曼增益 4)滤波 5)滤波误差方差阵 ③、模型概率更新 其中, 为归一化常数,且,而为观测的似然函数,。④、输出交互 三、仿真实验下载后可任意编辑设定目标运动起始位置坐标(x,y)为(1000,1000),初始速度为(10,10),采样间隔 T=1s ,CT 模型运动的角速度,即做顺时针匀速转弯运动。x 和 y 独立地进行观测,观测标准差为 50 米。目标在 1~150s 运动模型为 CV,151~270s 运动模型为 CT, 271~400s 运动模型为 CV。目标运动真实轨迹和测量轨迹如图 1 所示。图 1 目标运动轨迹在 IMM 滤波时,使用 2 个模型集,即 CV、CT,假设我们已经知道 CT 模型的目标运动角速度 w,Markov 转移矩阵。进行蒙特卡洛仿真,得到 IMM 滤波结果。将此滤波结果与单独的 CV、CT 模型的标准卡尔曼滤波结果对比,如图 2 所示。由图可知,CT 模型滤波结果与真实值有较大偏差,在转弯时 CV 模型卡尔曼滤波结果偏离偏离真实值,而 IMM 算法能较好的跟踪目标。下载后可任意编辑图 2 各种滤波结果图为了定量分析滤波结果,我们将 X、Y 方向的 CV、CT 卡尔曼滤波、IMM滤波与真实值分别求位置偏差、均方根误差并进行进行对比,如图 3、图 4 所示...