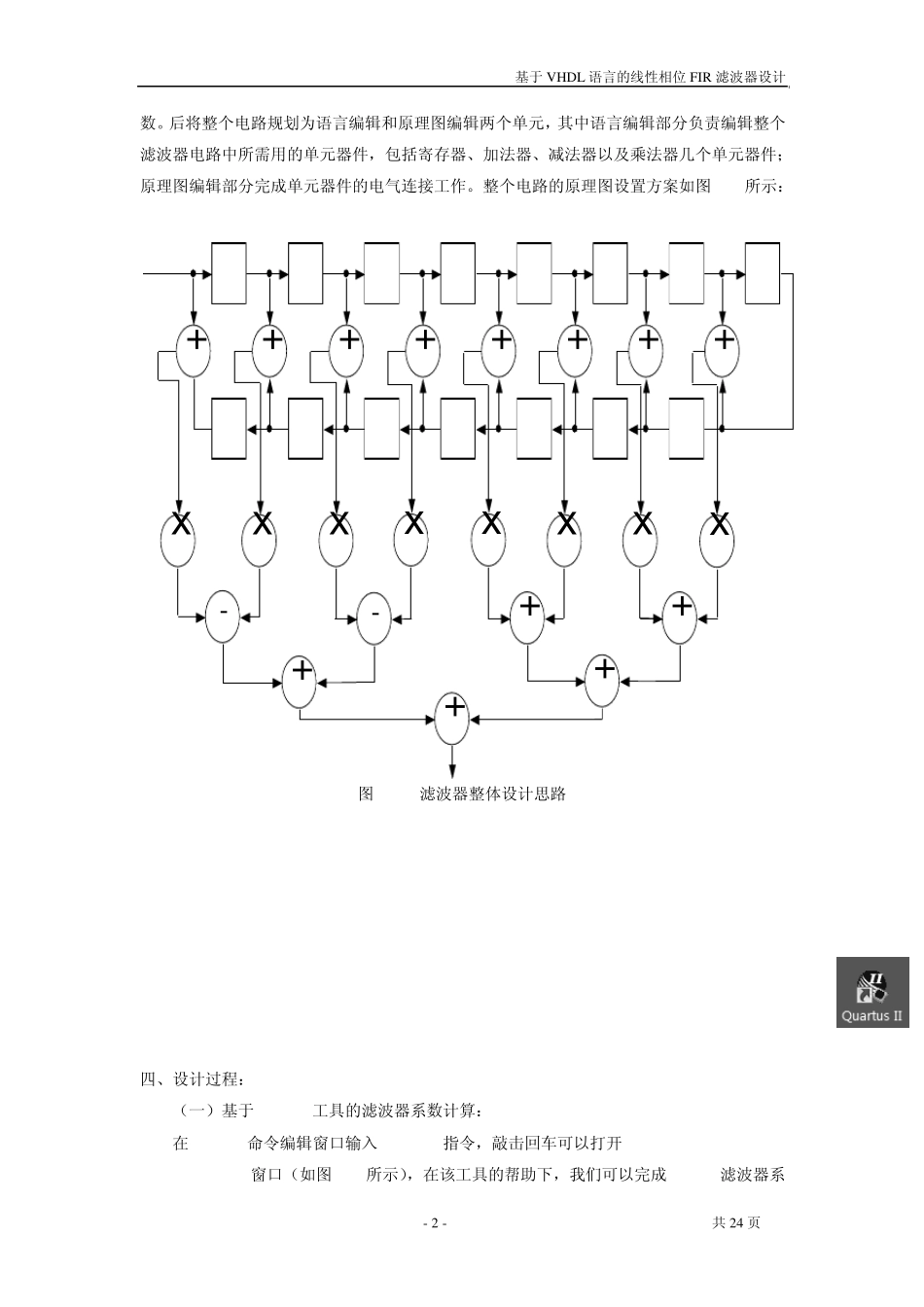
一、设计指标: 设计一个 16阶低通线性相位 FIR滤波器; 要求采样频率 Fs为 80KHz; 截止频率 Fc为 10KHz; 采用函数窗法设计,且窗口类型为 Kaiser,Beta为 0.5; 输入序列位宽为 10位的有符号数(最高位为符号位); 输出序列位宽为 10位的有符号数(最高位为符号位)。 二、线性相位 fir滤波器理论: 有限长脉冲响应(FIR)滤波器的系统函数只有零点,除原点外,没有极点,因而 FIR滤波器总是稳定的。如果他的单位脉冲响应是非因果的,总能够方便的通过适当的移位得到因果的单位脉冲响应,所以 FIR滤波器不存在稳定性和是否可实现的问题。它的另一个突出的优点是在满足一定的对称条件时,可以实现严格的线性相位。由于线性相位滤波器不会改变输入信号的形状,而只是在时域上使信号延时,因此线性相位特性在工程实际中具有非常重要的意义,如在数据通信、图像处理等应用领域,往往要求信号在传输和处理过程中不能有明显的相位失真,因而线性相位 FIR滤波器得到了广泛的应用。 长度为 M的因果有限冲激响应滤波器由传输函数 H(z)描述: 10( )( )MkkHzh k z (1) 它是次数为 M-1的 z-1的一个多项式。在时域中,上述有限冲激响应滤波器的输入输出关系为: 10( )( ) ()Mky nh k x nk (2) 其中 y(n)和 x(n)分别是输出和输入序列。 有限冲激响应滤波器的一种直接型实现,可由式(2)生成,M=5的情况如图 2-1(a)所示。其转置,如图 2-1(b)所示,是第二个直接型结构。通常一个长度为 M的有限冲激响应滤波器由 M个系数描述,并且需要 M个乘法器和(M-1)个双输入加法器来实现。 南京理工大学 EDA 技术与应用课程实验报告 - 1 - 共24 页 -1z-1z-1z-1z+x(n)h(0)h(1)h(2)h(3)h(4)y(n)+++ (a) h(0)h(1)h(2)h(3)h(4)-1z-1z-1z-1z++++x(n)y(n) (b) 图2- 1 直接型有限冲激响应滤波器结构 长度为M的线性相位有限冲激响应滤波器由对称的冲激响应h(n)= h(M-1-n)或反对称的冲激响应h(n)=-h(M-1-n)描述。利用线性相位有限冲激响应滤波器的对称(或反对称)性质,可以将传输函数的直接型实现所需的乘法器总量减少一半。例如,图2-2显示了一个具有对称冲击响应的、长度为7的有限冲激响应传输函数的实现。 -1z-1z-1z-1z-1z-1z+++h(0)h(1)h(2)h(3)++x(n)y(n)+ 图2- 2 线性相位有限冲激响应结构 三、设计思路: 根据课程...