《结构力学习题集》矩阵位移法习题及答案

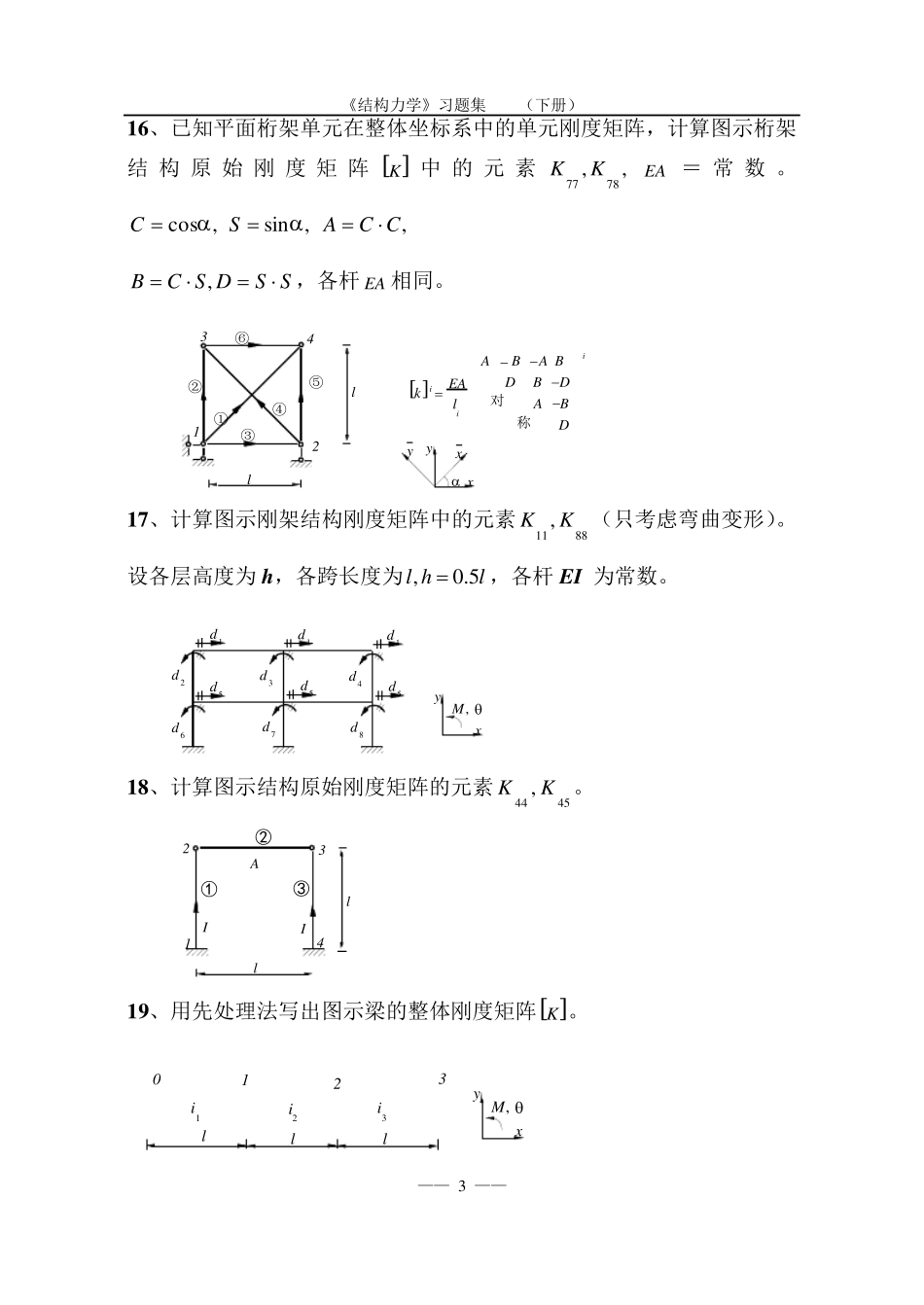
《结构力学》习题集 （下册） —— 1 —— 第八章 矩阵位移法 一、判断题： 1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。 2、单元刚度矩阵均具有对称性和奇异性。 3、局部坐标系与整体坐标系之间的坐标变换矩阵 T 是正交矩阵。 4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。 5、结构刚度方程矩阵形式为：    KP ，它是整个结构所应满足的变形条件。 6、图示结构用矩阵位移法计算时（计轴向变形）未知量数目为 8 个。 7、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。 8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。 9、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。 10、矩阵位移法既能计算超静定结构，也能计算静定结构。 11、已知图示刚架各杆 EI = 常数，当只考虑弯曲变形，且各杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是： (0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234xyM, ( ) 《结构力学》习题集 （下册） —— 2 —— 二、计算题： 1 2 、用先处理法计算图示结构刚度矩阵的元素1 33 32 2,,KKK。 123ll4ll5EI2EIEA(0 ,0 ,0 )(0 ,0 ,1 )(0 ,2 ,3 )(0 ,0 ,0 )(0 ,2 ,4 )(0 ,0 ,0 )xyM, EI 1 3 、用先处理法计算图示刚架结构刚度矩阵的元素1 53 42 2,,KKK。EI，EA 均为常数。 l(0 ,0 ,1 )(0 ,5 ,0 )(2 ,3 ,4 )l① ② 123xyM,  1 4 、计算图示结构整体刚度矩阵的元素6 65 54 4,,KKK。E 为常数。 lll1342A , IAA/222AI, 2 A xyM,  1 5 、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵 KK2 22 4,。 312① ② ③    kk1 11 2    kk2 12 2  kiiiii单刚分块形式为 ： 4xyM,  《结构力学》习题集 （下册） —— 3 —— 1 6 、已知平面桁架单元在整体坐标系中的单元刚度矩阵，计算图示桁架结构原 始 刚 度 矩 阵  K中 的 元 素,,7877 KKEA ＝ 常 数 。,cosC ,sin S,CCA SSDSCB,，各杆 EA 相同。 ll1342① ② ③ ④ ⑤ ⑥ xyxy kEAliABA BDBDABD ii...