一元二次方程知识点总结及典型习题

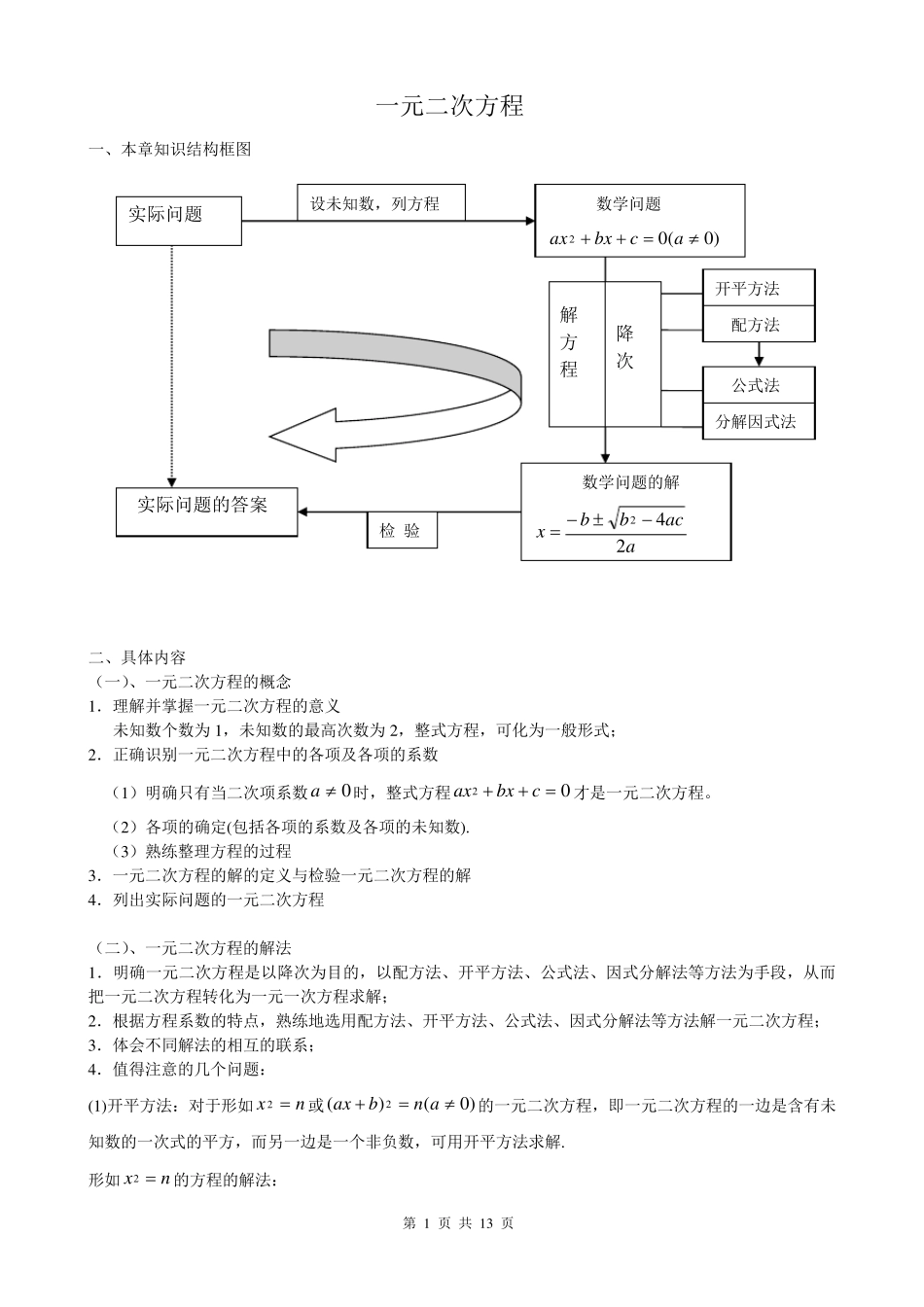
第 1 页 共 1 3 页 一元二次方程 一、本章知识结构框图 二、具体内容 （一）、一元二次方程的概念 1 ．理解并掌握一元二次方程的意义 未知数个数为 1 ，未知数的最高次数为 2 ，整式方程，可化为一般形式； 2 ．正确识别一元二次方程中的各项及各项的系数 （1 ）明确只有当二次项系数0a时，整式方程02cbxax才是一元二次方程。 （2 ）各项的确定(包括各项的系数及各项的未知数). （3 ）熟练整理方程的过程 3 ．一元二次方程的解的定义与检验一元二次方程的解 4 ．列出实际问题的一元二次方程 （二）、一元二次方程的解法 1 ．明确一元二次方程是以降次为目的，以配方法、开平方法、公式法、因式分解法等方法为手段，从而把一元二次方程转化为一元一次方程求解； 2 ．根据方程系数的特点，熟练地选用配方法、开平方法、公式法、因式分解法等方法解一元二次方程； 3 ．体会不同解法的相互的联系； 4 ．值得注意的几个问题： (1 )开平方法：对于形如nx 2或)0()(2anbax的一元二次方程，即一元二次方程的一边是含有未知数的一次式的平方，而另一边是一个非负数，可用开平方法求解. 形如nx 2的方程的解法： 实际问题 数学问题 )0(02acbxax 设未知数，列方程 实际问题的答案 数学问题的解 aacbbx242  解 方 程 降 次 开平方法 配方法 公式法 分解因式法 检 验 第 2 页 共 13 页 当0n时， nx; 当0n时，021 xx; 当0n时，方程无实数根。 （2）配方法：通过配方的方法把一元二次方程转化为nmx2)(的方程，再运用开平方法求解。 配方法的一般步骤： ①移项：把一元二次方程中含有未知数的项移到方程的左边，常数项移到方程的右边； ②“系数化1”：根据等式的性质把二次项的系数化为1； ③配方：将方程两边分别加上一次项系数一半的平方，把方程变形为nmx2)(的形式； ④求解：若0n时，方程的解为nmx，若0n时，方程无实数解。 （3）公式法：一元二次方程)0(02acbxax的根aacbbx242  当042 acb时，方程有两个实数根,且这两个实数根不相等； 当042 acb时，方程有两个实数根,且这两个实数根相等，写为abxx221； 当042 acb时，方程无实数根. 公式法的一般步骤：①把一元二次方程化为一般式；②确定cba,,的值；③代入acb42 中计算其值，判断方程是否有实数根；④若0...