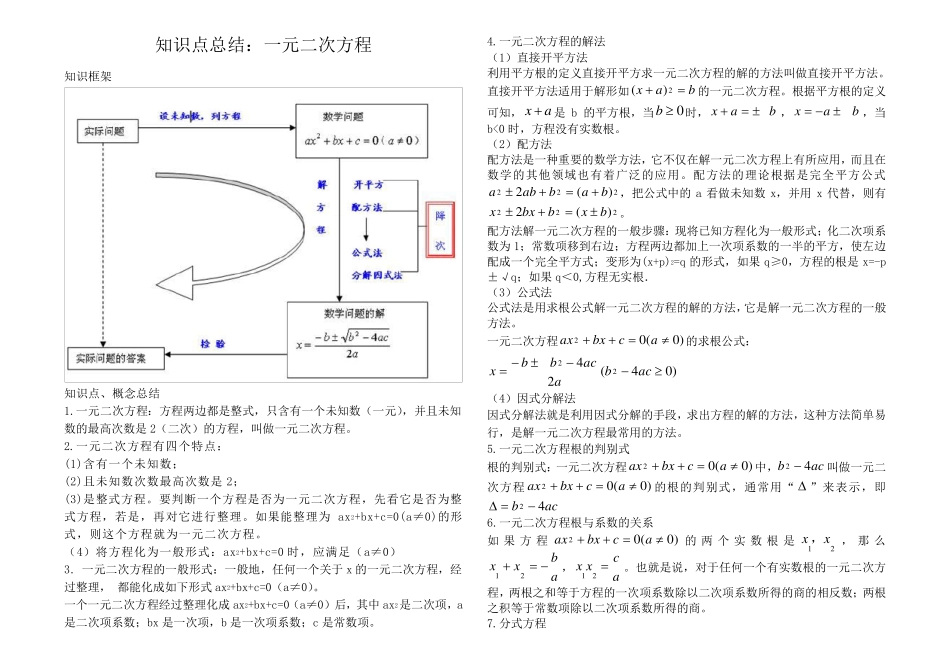
知识点总结:一元二次方程 知识框架 知识点、概念总结 1.一元二次方程:方程两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程。 2.一元二次方程有四个特点: (1)含有一个未知数; (2)且未知数次数最高次数是2; (3)是整式方程。要判断一个方程是否为一元二次方程,先看它是否为整式方程,若是,再对它进行整理。如果能整理为 ax2+bx+c=0(a≠0)的形式,则这个方程就为一元二次方程。 (4)将方程化为一般形式:ax2+bx+c=0 时,应满足(a≠0) 3. 一元二次方程的一般形式:一般地,任何一个关于x 的一元二次方程,经过整理,•都能化成 如下 形式ax2+bx+c=0(a≠0)。 一个一元二次方程经过整理化成 ax2+bx+c=0(a≠0)后 ,其 中 ax2是二次项 ,a是二次项 系 数;bx 是一次项 ,b 是一次项 系 数;c 是常 数项 。 4.一元二次方程的解 法 (1)直 接 开 平 方法 利 用 平 方根 的定 义 直 接 开 平 方求 一元二次方程的解 的方法 叫做直 接 开 平 方法 。直 接 开 平 方法 适 用 于解 形如bax2)(的一元二次方程。根 据 平 方根 的定 义可 知,ax是b 的平 方根 ,当0b时,bax,bax,当b<0 时,方程没 有实 数根 。 (2)配 方法 配 方法 是一种 重 要的数学 方法 ,它不 仅 在 解 一元二次方程上 有所 应用 ,而 且在数学 的其 他 领 域 也 有着 广 泛 的应用 。配 方法 的理论 根 据 是完 全 平 方公 式222)(2bababa,把 公 式中 的a 看做未知数x,并用x 代替,则有222)(2bxbbxx。 配 方法 解 一元二次方程的一般步骤:现将已知方程化为一般形式;化二次项 系数为1;常 数项 移到右边;方程两边都加上 一次项 系 数的一半的平 方,使左边配 成 一个完 全 平 方式;变形为(x+p)2=q 的形式,如果q≥0,方程的根 是x=-p±√q;如果q<0,方程无实 根 . (3)公 式法 公 式法 是用 求 根 公 式解 一元二次方程的解 的方法 ,它是解 一元二次方程的一般方法 。 一元二次方程)0(02acbxax的求 根 公 式: )04(2422acbaacbbx (4)因式分解 法 因式分解 法 就是利 用 因式分解 的手段,求 出方程的解 的方法 ,这种 方法 简单易行,是解 一元二次方程最常 用 ...