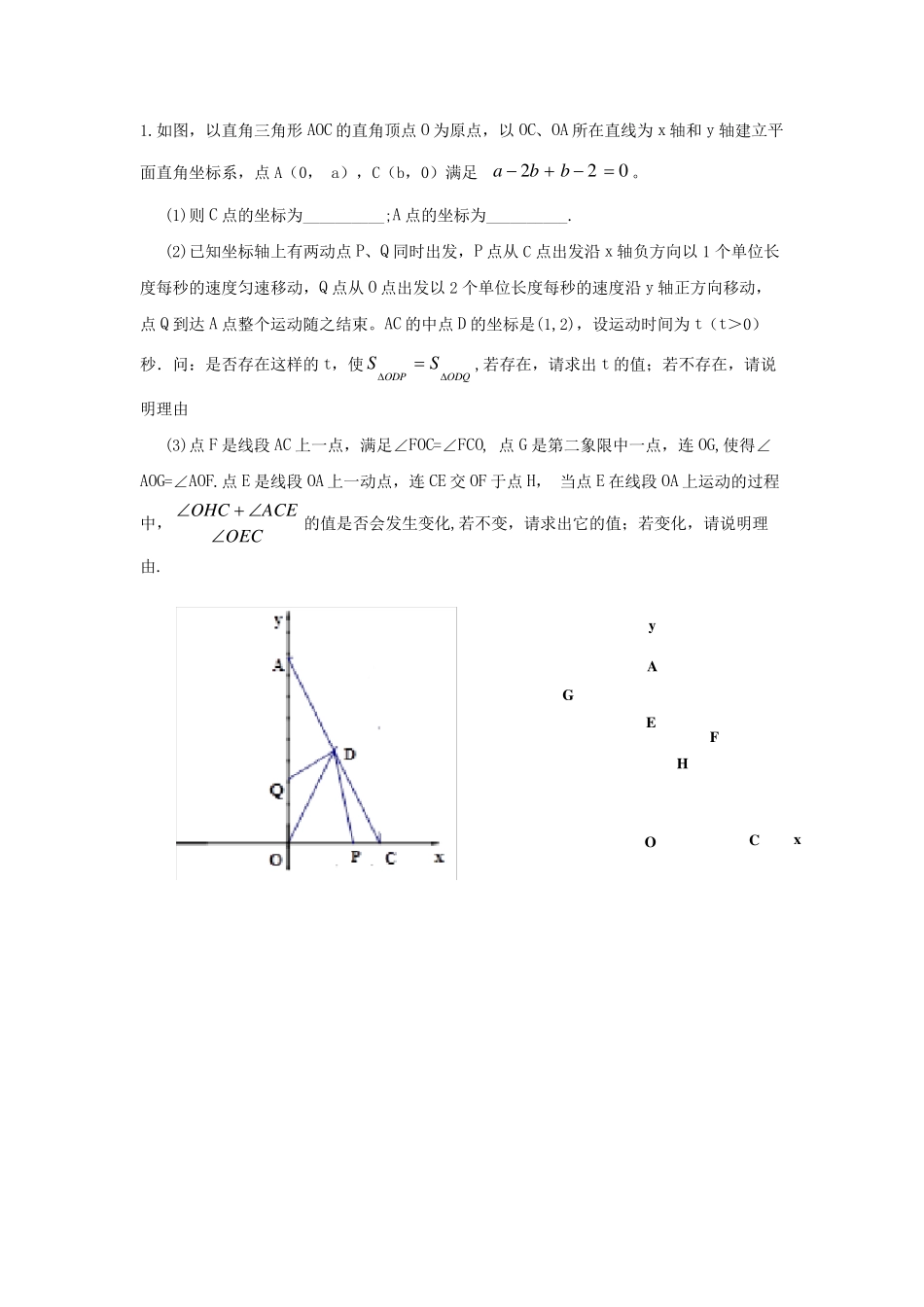
1.如图,以直角三角形AOC 的直角顶点O 为原点,以OC、OA 所在直线为x 轴和y 轴建立平面直角坐标系,点A(0, a),C(b,0)满足022bba。 (1)则C 点的坐标为__________;A 点的坐标为__________. (2)已知坐标轴上有两动点P、Q 同时出发,P 点从C 点出发沿x 轴负方向以1 个单位长度每秒的速度匀速移动,Q 点从O 点出发以2 个单位长度每秒的速度沿y 轴正方向移动,点Q 到达A 点整个运动随之结束。AC 的中点D 的坐标是(1,2),设运动时间为t(t>0)秒.问:是否存在这样的t,使ODQODPSS,若存在,请求出t 的值;若不存在,请说明理由 (3)点F 是线段AC 上一点,满足∠FOC=∠FCO, 点G 是第二象限中一点,连 OG,使得∠AOG=∠AOF.点E 是线段OA 上一动点,连 CE 交 OF 于点H, 当点E 在线段OA 上运动的过程中, OECACEOHC的值是否会发生变化,若不变,请求出它的值;若变化,请说明理由. HGFExACOy2.在平面直角坐标系中,直线l 与x 轴、y 轴分别交于A、B 两点,且直线上所有点的坐标(x 、y )都是二元一次方程01 23-4yx的解.(P109) (1)求A、B 两点坐标; (2)如图1:把线段BA 绕B 点顺时针旋转,点A 的对应点为C 点,使BC⊥y 轴,E 为线段AC 上一点,EN⊥AB 于N,EM⊥BC 于M,求EM+EN 的值. (3)如图2:点D 为y 轴上点B 上方一点,DE⊥AD 交直线CB 于点E,∠DEC 的平分线EF与∠DAO 的邻补角的平分线AF 交点F,请问:D 点在运动的过程中∠AFE 的大小是否变化,若不变,求出其值;若变化,请说明理由. 3.在平面直角坐标系中,点A(0,a)、B(b,0)、C(c,c)的坐标满足(a-5)2+|b+2|+3c=0,四边形 ABCD是平行四边形,点D 在第一象限,直线AC 交x 轴于点F (1) 求点D 的坐标 (2) 求证:∠DCF=∠ABF+∠AFB (3) 求ACCF 的比值 4.如乙图,长方形ABCD 在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).点X,Y 分别在x,y 轴上. (1)请直接写出D 点的坐标 . (2)连接线段OB,OD,OD 交BC 于E,如甲图,∠BOY 的平分线和∠BEO 的平分线交于点F,若∠BOE=n,∠OFE 的度数. (3)若长方形ABCD 以每秒个单位的速度向下运动,设运动的时间为t 秒,问第一象限内是否存在某一时刻t,使△OBD 的面积等于长方形ABCD 的面积的?若存在,请求出t的值;若不存在,请说明理由. 5.如图1 所示,△ABC 的三条边是三块...