三角函数的图像与性质(比较全)

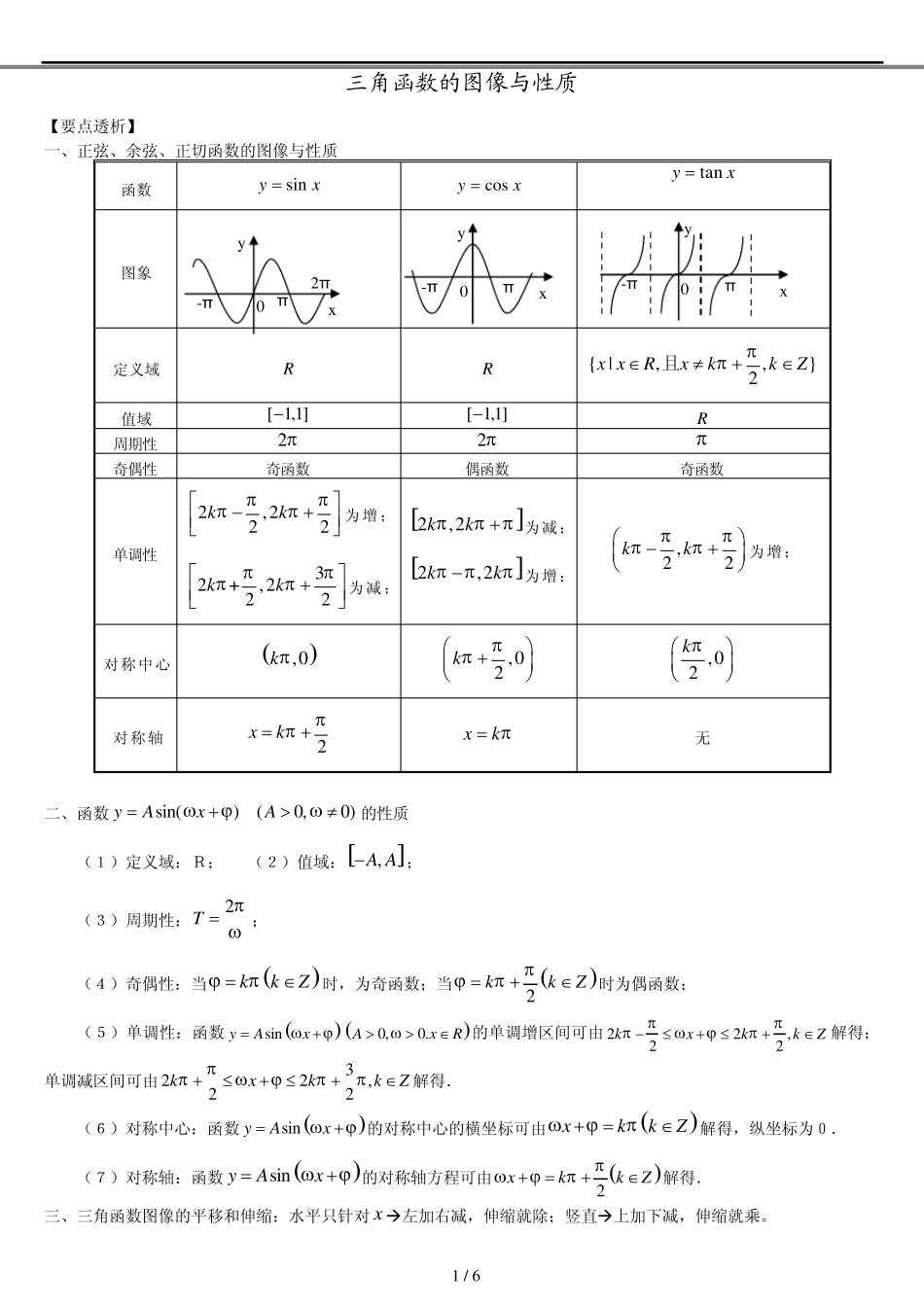
1 / 6 三角函数的图像与性质 【要点透析】 一、正弦、余弦、正切函数的图像与性质 二、函数sin()(0,0)yAxA的性质 （１）定义域：Ｒ； （２）值域：,A A； （３）周期性：2T； （４）奇偶性：当kkZ时，为奇函数；当2kkZ时为偶函数； （５）单调性：函数sinyAx0,0.AxR的单调增区间可由 22,22kxkkZ解得；单调减区间可由322,22kxkkZ解得． （６）对称中心：函数sinyAx的对称中心的横坐标可由xkkZ解得，纵坐标为０． （７）对称轴：函数sinyAx的对称轴方程可由2xkkZ解得． 三、三角函数图像的平移和伸缩：水平只针对 x左加右减，伸缩就除；竖直上加下减，伸缩就乘。 函数 sinyx cosyx tanyx 图象 定义域 R R { |,,}2x xRxkkZ且 值域 [ 1,1] [ 1,1] R 周期性 2 2  奇偶性 奇函数 偶函数 奇函数 单调性 2,222kk为增；32+,222kk为减； 2,2kk为减；2,2kk为增； ,22kk为增； 对称中心 ,0k ,02k ,02k 对称轴 2xk xk 无 x -π π 2π 0 y x π y -π 0 y -π π x 0 2 / 6 【常考题型总结】 题型一、三角函数图像、定义域、值域 例1、作函数21 cosyx的图象． 变式、作函数sin(2)3yx的图像 例2、求下列函数的定义域： （1）sin 2yx； （2）cos()3yx； （3）sinyx； （4） 1sin1yx； （5）225lgsinyxx． 例3、求使下列函数取得最大值的自变量x 的集合，并说出最大值是什么？ （1）cos1yx ，xR； （2）sin 2yx，xR． 变式、求下列函数的值域：（1）21sin1yx； （2）sinsin2xyx；(3)23cos4sin4,[,]3 3yxxx   课堂作业1、（1）2sin1sinxyx；（2）cos3cos2xyx；(3) 2tan3tan1yxx 2、已知函数22cos2 cos(21)yxaxa。⑴求函数的最小值( )f a ；⑵试确定满足1( )2f a 的a 的值； ⑶当a 取⑵中的值时，求y 的最大值 题型二、三角函数周期 例1、求下列函数周期：（1...