三角函数的图像与性质知识点及题型归纳总结

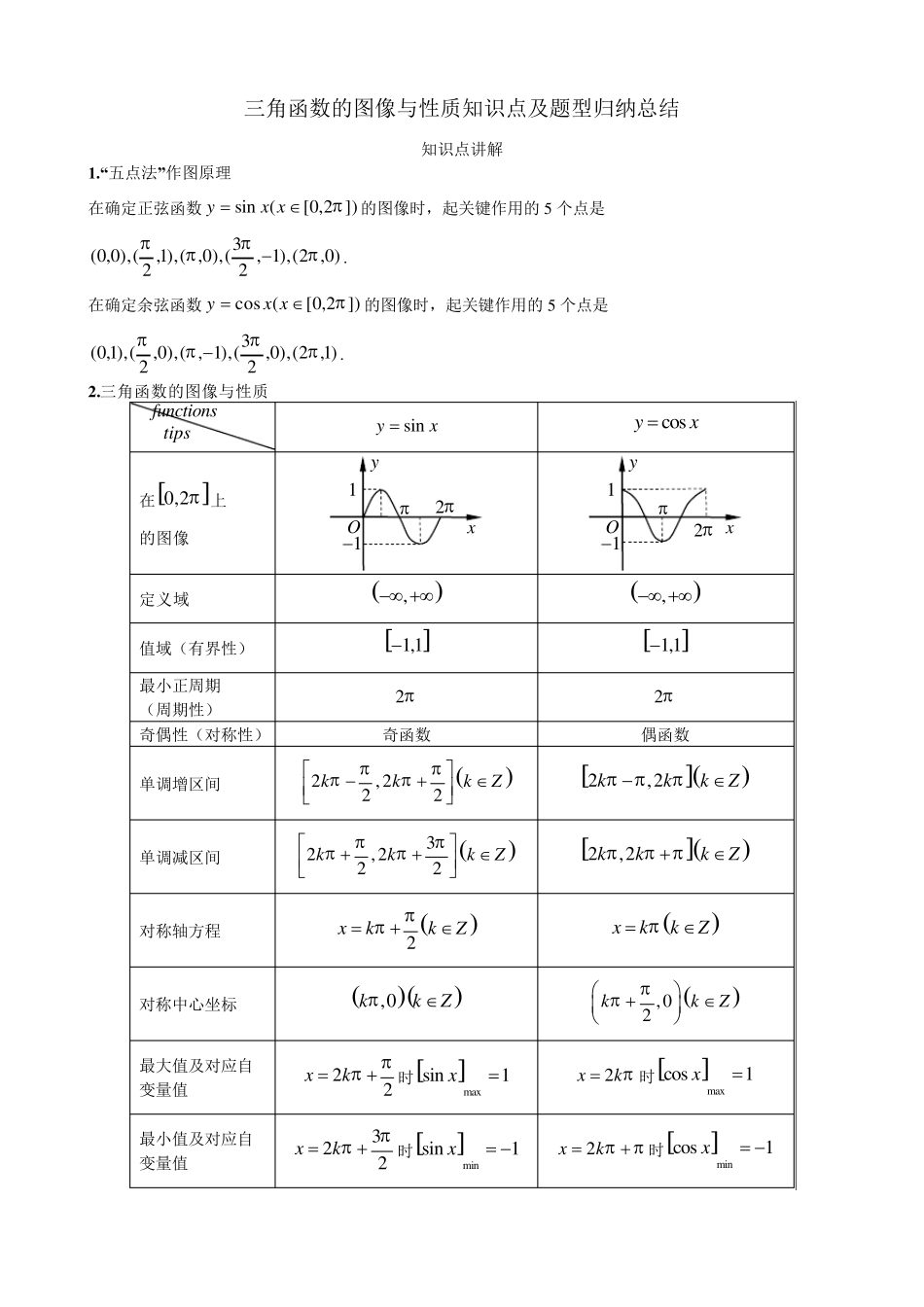
三角函数的图像与性质知识点及题型归纳总结 知识点讲解 1.“五点法”作图原理 在确定正弦函数])2,0[(sinxxy的图像时，起关键作用的 5 个点是)0,2(),1,23(),0,(),1,2(),0,0(. 在确定余弦函数])2,0[(cosxxy的图像时，起关键作用的 5 个点是)1,2(),0,23(),1,(),0,2(),1,0(. 2 .三角函数的图像与性质 sinyx cosyx 在0,2 上 的图像 定义域 ,  ,  值域（有界性） 1,1 1,1 最小正周期 （周期性） 2 2 奇偶性（对称性） 奇函数 偶函数 单调增区间 2,222kkkZ 2,2kkkZ 单调减区间 32,222kkkZ 2,2kkkZ 对称轴方程 2xkkZ xkkZ 对称中心坐标 ,0kkZ ,02kkZ 最大值及对应自变量值 22xk时maxsin1x 2xk时maxcos1x 最小值及对应自变量值 322xk时minsin1x  2xk时mincos1x  xyO112xyO112functionstips函数 正切函数tan ,2yx xk 图像 定义域 |,2x xkkZ 值域 ),( 周期性 T 奇偶性 奇函数，图像关于原点对称 单调性 在(,),()22kkkZ上是单调增函数 对称轴 无 对称中心 ,0 ()2kkZ 3.)sin(wxAy与)0,0)(cos(wAwxAy的图像与性质 （1）最小正周期：wT2. （2）定义域与值域：)sin(wxAy，）wxAycos(的定义域为R，值域为[-A,A]. （3）最值 假设00wA，. ①对于)sin(wxAy， ;)(22;)Z(22AZkkwxAkkwx时，函数取得最小值当时，函数取得最大值当 ②对于）wxAycos(， ;)(2;)Z(2AZkkwxAkkwx时，函数取得最小值当时，函数取得最大值当 （4）对称轴与对称中心. 假设00wA，. ①对于)sin(wxAy， xOy).0,()sin(0)sin()()sin(1)sin()(2000000xwxywxZkkwxxxwxywxZkkwx的对称中心为时，，即当的对称轴为时，，即当 ②对于）wxAycos(， ...