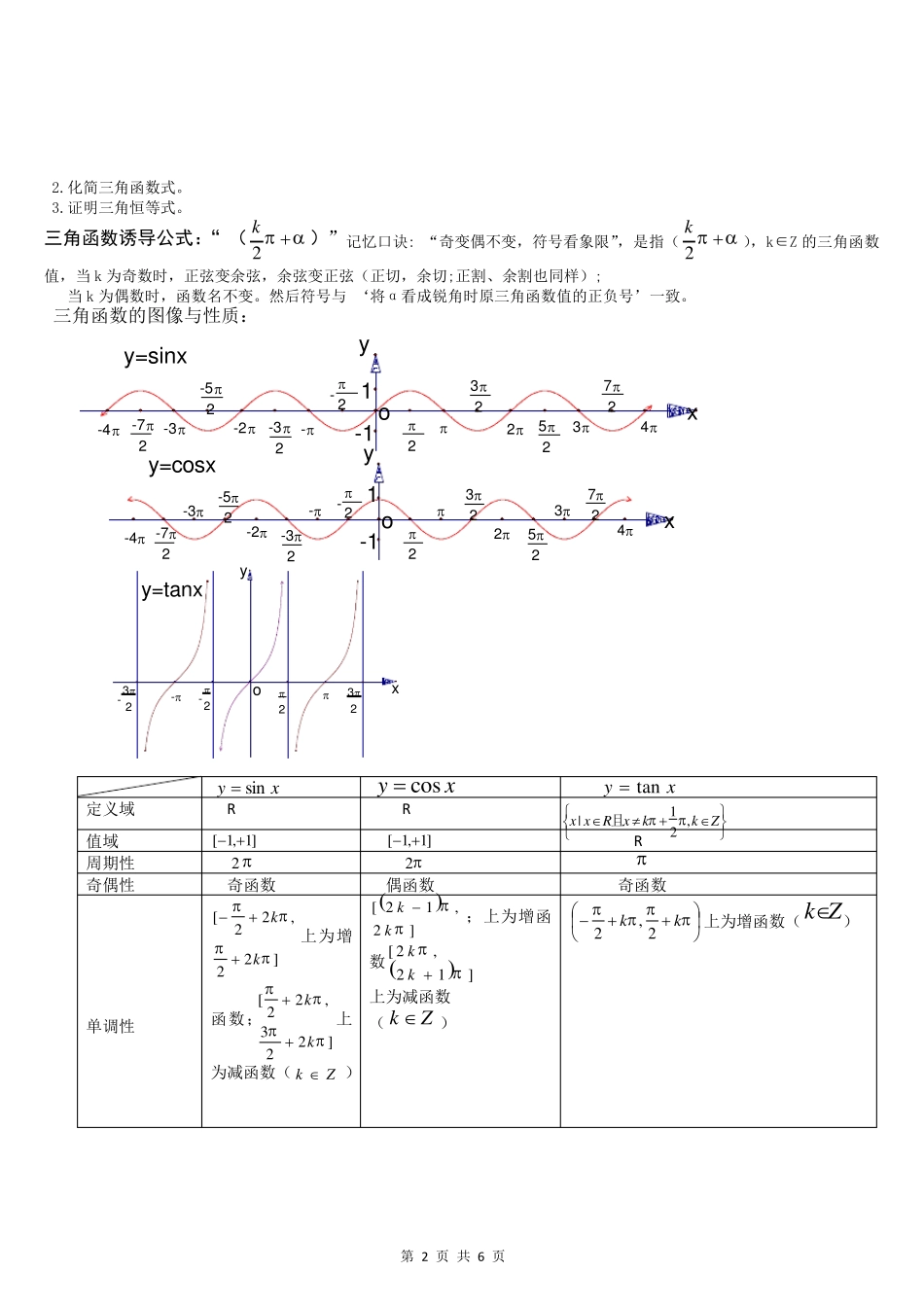
第 1 页 共 6 页 教 学 内 容 : 任 意 角 三 角 函 数 、 三 角 函 数 的 诱 导 公 式 、 图 像 及 性 质 教 学 目 标 : 熟 练 掌 握 三 块 的 知 识 点 及 基 本 题 型 教 学 重 点 : 任 意 角 三 角 函 数 、 三 角 函 数 的 诱 导 公 式 教 学 难 点 : 三 角 函 数 的 诱 导 公 式 教 学 过 程 : 1 . 知 识 要 点 角的概念的推广: 平 面 内 一 条 射 线 绕 着 端 点 从 一 个 位 置 旋 转 到 另 一 个 位 置 所 的 图 形 。 按 逆 时 针 方 向 旋 转 所 形 成 的 角 叫 正 角 , 按 顺 时 针 方 向旋 转 所 形 成 的 角 叫 负 角 , 一 条 射 线 没 有 作 任 何 旋 转 时 , 称 它 形 成 一 个 零 角 。 射 线 的 起 始 位 置 称 为 始 边 , 终 止 位 置 称 为 终 边 。 象限角的概念: 在 直 角 坐 标 系 中 , 使 角 的 顶 点 与 原 点 重 合 , 角 的 始 边 与 x 轴 的 非 负 半 轴 重 合 , 角 的 终 边 在 第 几 象 限 , 就 说 这 个 角 是 第 几象 限 的 角 。 如 果 角 的 终 边 在 坐 标 轴 上 , 就 认 为 这 个 角 不 属 于 任 何 象 限 。 终边相同的角的表示: 终 边 与 终 边 相 同 ( 的 终 边 在 终 边 所 在 射 线 上 )2()kkZ 。 注意: 相 等 的 角 的 终 边 一 定 相 同 , 终 边 相 同 的 角 不 一 定 相 等 . 终 边 在 x 轴 上 的 角 可 表 示 为 :,kkZ; 终 边 在 y 轴 上 的 角 可 表 示 为 :,2kkZ; 终 边 在 坐 标 轴 上 的 角 可 表 示 为 :,2kkZ . 角 度 与 弧 度 的 互 换 关系 : 360°=2 180°= 1°=0.01745 1=57.30°=57°18′ 注意 : 正 角 的 弧 度 数 为 正 数 , 负 角 的 弧 度 数 为 负 数 , 零 角 的 弧 度 数 为 零 . 与2 的终边关系: 任意角的三角函数的定义: 设 是 任 意 一 个 角 , P ( , )x y 是 的 终 边 上 的 任...