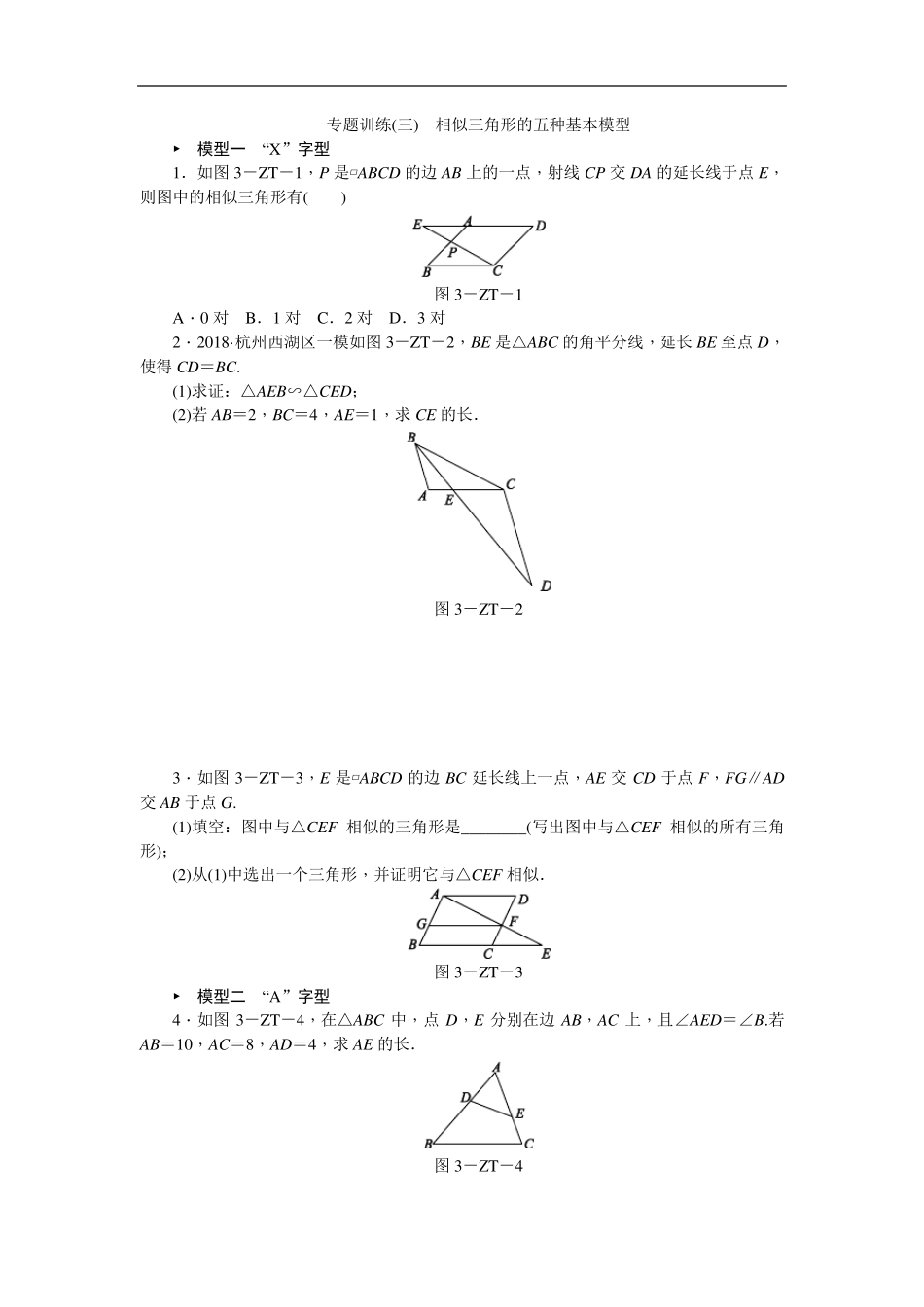
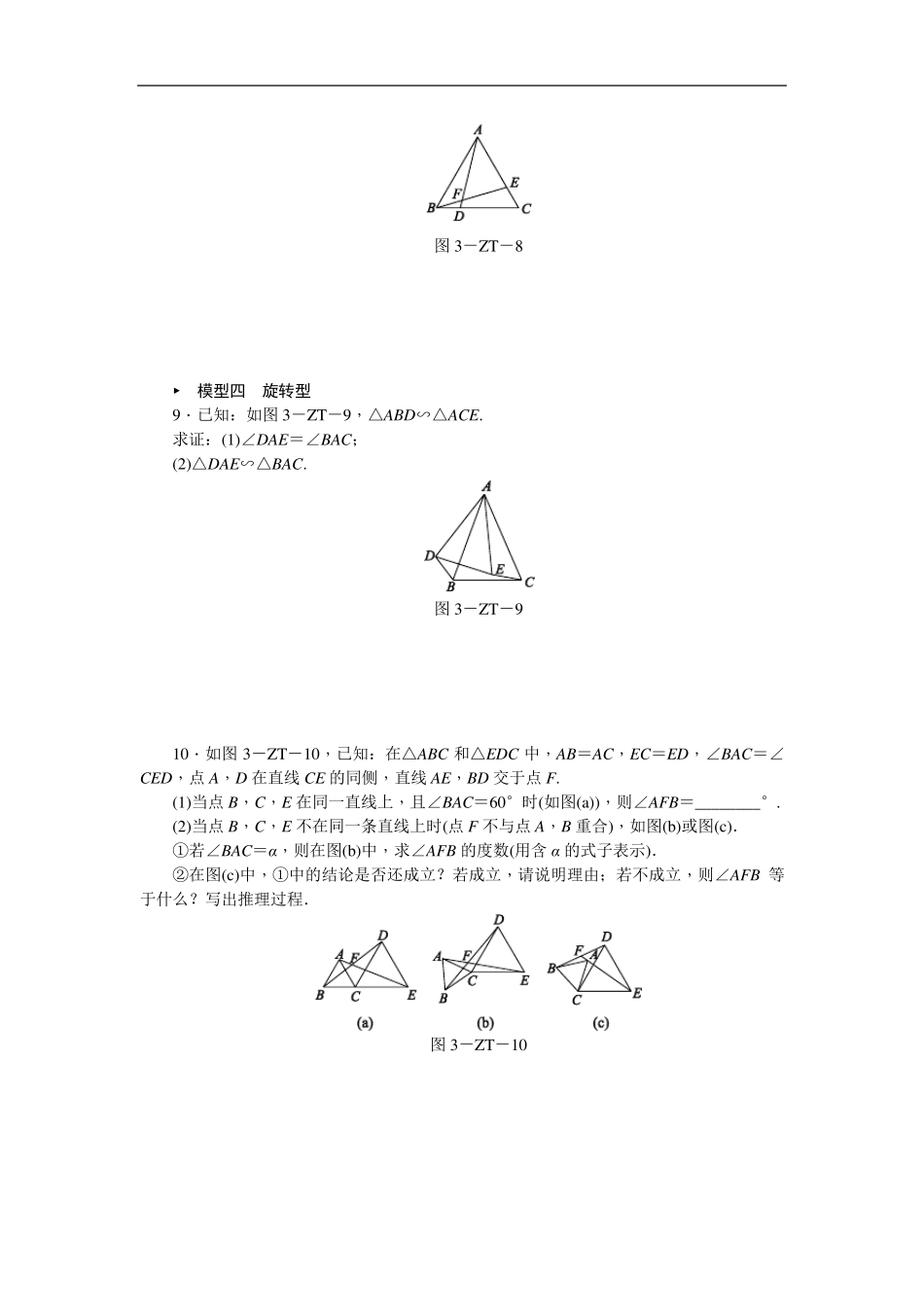
专题训练(三) 相似三角形的五种基本模型 ► 模型一 “X”字型 1.如图 3-ZT-1,P 是▱ABCD 的边 AB 上的一点,射线 CP 交 DA 的延长线于点 E,则图中的相似三角形有( ) 图 3-ZT-1 A.0 对 B.1 对 C.2 对 D.3 对 2.2018·杭州西湖区一模如图 3-ZT-2,BE 是△ABC 的角平分线,延长 BE 至点 D,使得 CD=BC. (1)求证:△AEB∽△CED; (2)若 AB=2,BC=4,AE=1,求 CE 的长. 图 3-ZT-2 3.如图 3-ZT-3,E 是▱ABCD 的边 BC 延长线上一点,AE 交 CD 于点 F,FG∥AD交 AB 于点 G. (1)填空:图中与△CEF 相似的三角形是________(写出图中与△CEF 相似的所有三角形); (2)从(1)中选出一个三角形,并证明它与△CEF 相似. 图 3-ZT-3 ► 模型二 “A”字型 4.如图 3-ZT-4,在△ABC 中,点 D,E 分别在边 AB,AC 上,且∠AED=∠B.若AB=10,AC=8,AD=4,求 AE 的长. 图 3-ZT-4 5.如图3-ZT-5,在△ABC 中,∠C=90°,AC=6 cm,BC=8 cm,点 D 从点 C 出发,以 2 cm/s 的速度沿折线 C-A-B 向点 B 运动,同时,点 E 从点 B 出发,以 1 cm/s 的速度沿 BC 边向点 C 运动,设点 E 运动的时间为 t(s)(0<t<8). (1)求 AB 的长; (2)当△BDE 是直角三角形时,求 t的值. 图3-ZT-5 ► 模型三 子母型 6.如图3-ZT-6 所示,点 D 在△ABC 的边 AB 上,AD=2,BD=4,AC=2 3. 求证:△ACD∽△ABC. 图3-ZT-6 7.如图3-ZT-7,CD 是 Rt△ABC 的斜边 AB 上的高,E 是 BC 上任意一点,EF⊥AB于点 F. 求证:AC2=AD·AF+CD·EF. 图3-ZT-7 8.如图3-ZT-8,△ABC 是等边三角形,点 D,E 分别在BC,AC 上,且 BD=CE,AD 与 BE 相交于点 F. (1)△AEF 与△ABE 相似吗?说明你的理由. (2)BD2=AD·FD 吗?请说明理由. 图3-ZT-8 ► 模型四 旋转型 9.已知:如图3-ZT-9,△ABD∽△ACE. 求证:(1)∠DAE=∠BAC; (2)△DAE∽△BAC. 图3-ZT-9 10.如图3-ZT-10,已知:在△ABC 和△EDC 中,AB=AC,EC=ED,∠BAC=∠CED,点A,D 在直线CE的同侧,直线AE,BD 交于点F. (1)当点B,C,E在同一直线上,且∠BAC=60°时(如图(a)),则∠AFB=________°. (2)当点B,C,E不在同一条直线上时(点F不与点A,B 重合),如图(b)或图(c). ①若∠BAC=α,则在图...