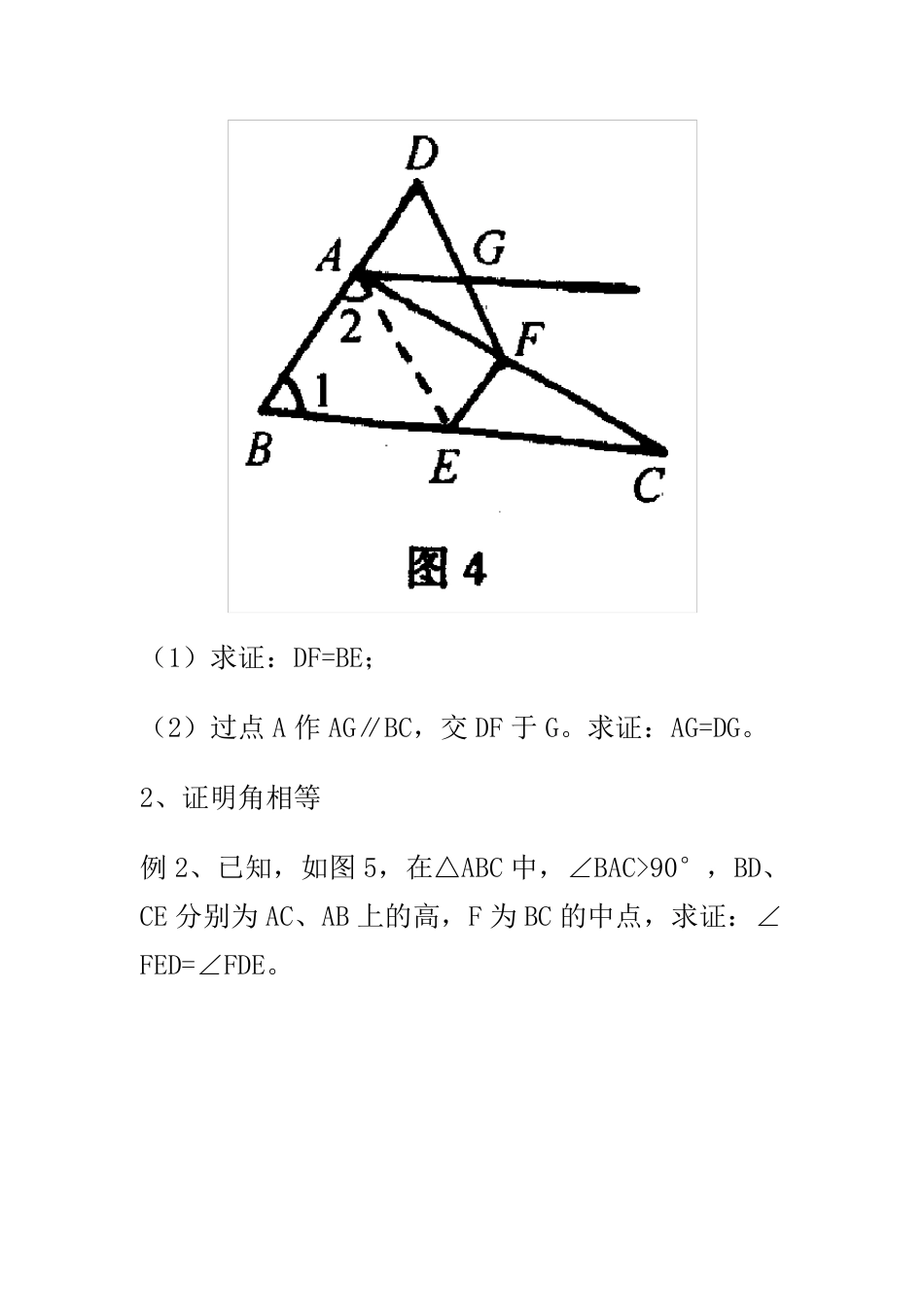
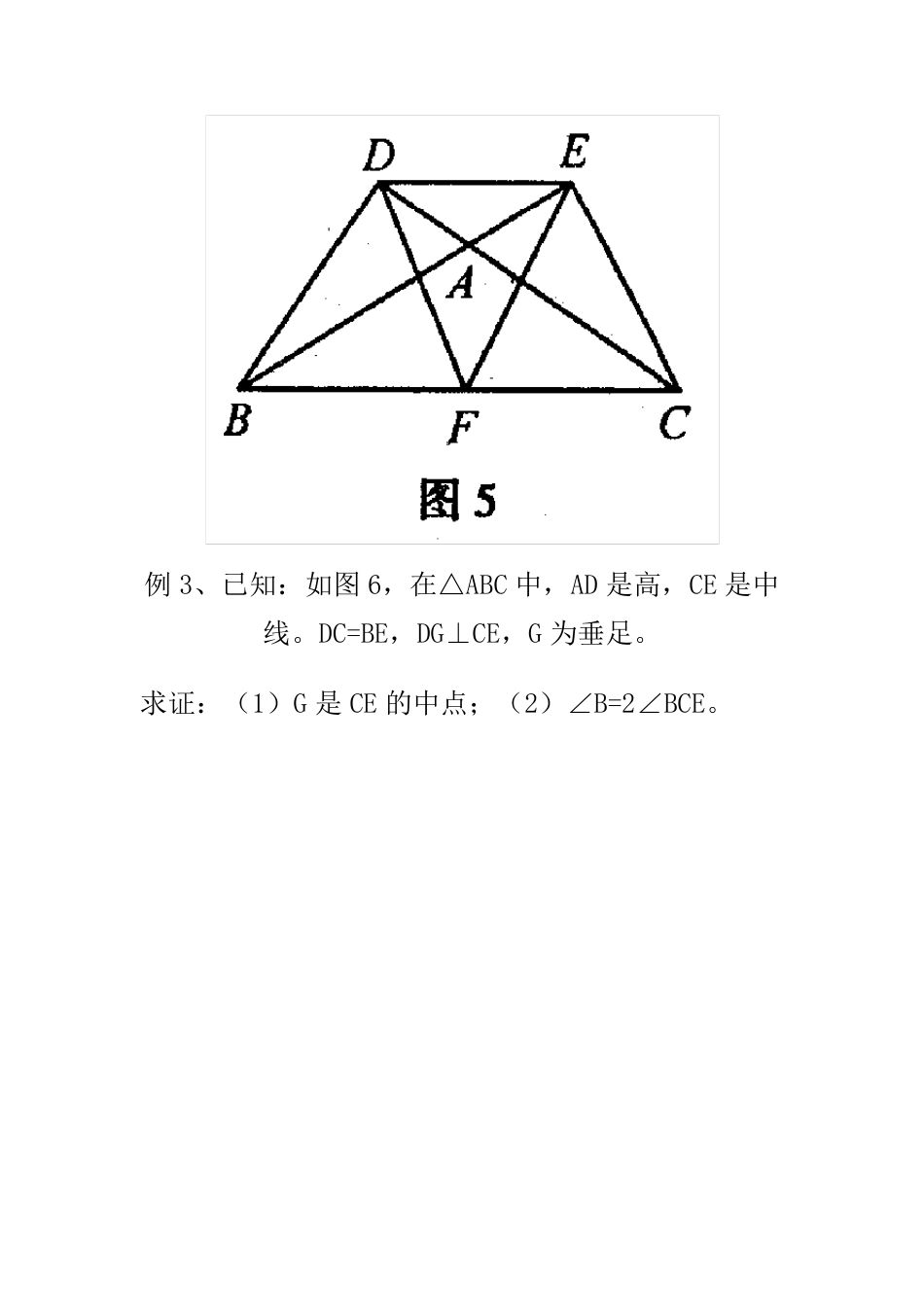
《直角三角形斜边上的中线等于斜边的一半》 专题训练 直角三角形斜边上中线的性质是直角三角形的一个重要性质,同时也是常考的知识点.它为证明线段相等、角相等、线段的倍分等问题提供了很好的思路和理论依据。 一、直角三角形斜边上中线的性质 性质:直角三角形斜边上的中线等于斜边的一半. 定理的证明 证明:直角三角形斜边上的中线等于斜边的一半. 二、性质的证明 1、证明线段相等 例1、如图4,在△ABC 中,∠BAC=90 °,延长 BA 到 D点,使,点E、F 分别为边BC、AC 的中点。 (1)求证:DF=BE; (2)过点A 作AG∥BC,交DF 于G。求证:AG=DG。 2、证明角相等 例2、已知,如图5,在△ABC 中,∠BAC>90°,BD、CE 分别为 AC、AB 上的高,F 为 BC 的中点,求证:∠FED=∠FDE。 例3、已知:如图6,在△ABC 中,AD 是高,CE 是中线。DC=BE,DG⊥CE,G 为垂足。 求证:(1)G 是CE 的中点;(2)∠B=2∠BCE。 3、证明线段的倍分及和差关系 例4、如图7,在△ABC 中,∠C=2∠B,D 是 BC 上的一点,且 AD⊥AB,点 E 是 BD 的中点,连 AE。求证:(1)∠AEC=∠C;(2)求证:BD=2AC。 例5、如图8,在梯形ABCD 中,AB∥CD,∠A+∠B=90°,E、F 分别是 AB、CD 的中点。求证:。 4、证明线段垂直 例6、如图9,在四边形ABCD 中,AC⊥BC,BD⊥AD,且 AC=BD,M、N 分别是 AB、DC 边上的中点。 求证:MN⊥DC。 5、证明特殊的几何图形 例7、如图10,将Rt△ACB 沿直角边AC 所在直线翻折180°得到 Rt△ACE,点 D 与点 F 分别是斜边AB、AE的中点,连 CD、CF,则四边形 ADCF 为菱形.请给予证明. 强化训练 1、如图,在锐角三角形 ABC 中,AD⊥BC 于 D,E、F、G 分别是 AC、AB、BC 的中点。 求证:四边形 O EFG 是等腰梯形。 FEGDCBA 2、如图所示,BD、CE 是三角形ABC 的两条高,M、N分别是BC、DE 的中点 求证:MN⊥DE NMEDCBA 3、已知梯形ABCD 中,∠B+∠C=90o,EF 是两底中点的连线,试说明 AB-AD=2EF FEDCBA 4、如图,四边形ABCD 中,∠DAB=∠DCB=90o,点M、N 分别是 BD、AC 的中点。MN、AC 的位置关系如何?证明你的猜想。 NMDCBA 5、过矩形ABCD 对对角线 AC 的中点 O 作 EF⊥AC分别交AB、DC 于E、F,点G 为AE 的中点,若∠AOG=30o 求证:3OG=DC GOFEDCBA6、如图所示;过矩形 ABCD 的顶点A 作一直线,交BC 的延长线于点E,F 是 AE 的中点,连接 FC、FD。 求证:∠FDA=∠FCB FDECBA