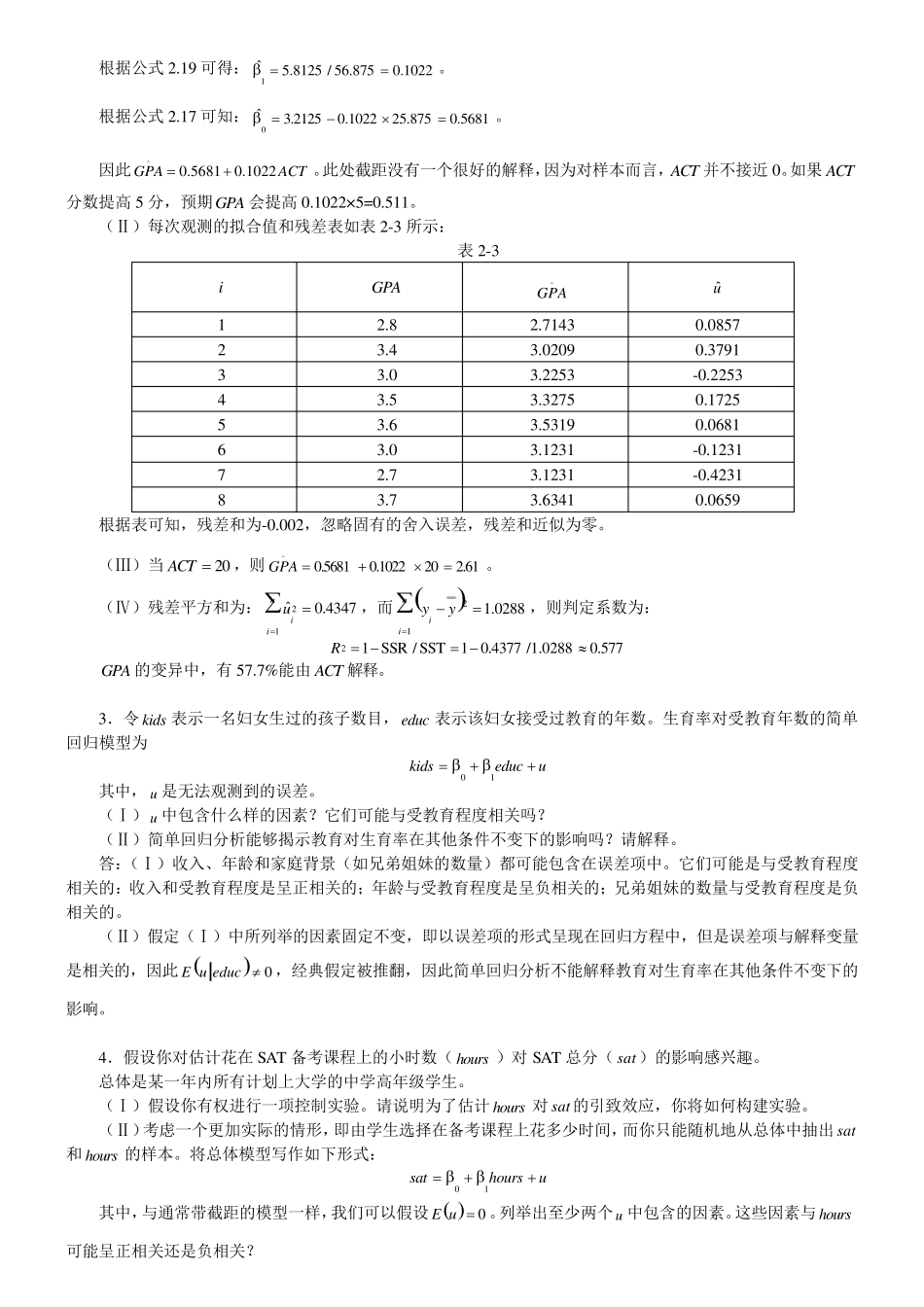
使用普通最小二乘法,此时最小化的残差平方和为 211niiiyx 利用一元微积分可以证明,1 必须满足一阶条件 110niiiixyx 从而解出1 为: 1121niiiniix yx 当且仅当0x 时,这两个估计值才是相同的。 2 .2 课后习题详解 一、习题 1.在简单线性回归模型01yxu 中,假定 0E u 。令 0E u ,证明:这个模型总可以改写为另一种形式:斜率与原来相同,但截距和误差有所不同,并且新的误差期望值为零。 证明:在方程右边加上 0E u ,则 0010yxu 令新的误差项为0eu ,因此 0E e 。 新的截距项为00,斜率不变为1 。 2.下表包含了8 个学生的ACT 分数和GPA(平均成绩)。平均成绩以四分制计算,且保留一位小数。 stu dent GPA ACT 1 2.8 21 2 3.4 24 3 3.0 26 4 3.5 27 5 3.6 29 6 3.0 25 7 2.7 25 8 3.7 30 (Ⅰ)利用OLS 估计GPA 和ACT 的关系;也就是说,求出如下方程中的截距和斜率估计值 01ˆˆGPAACT^ 评价这个关系的方向。这里的截距有没有一个有用的解释?请说明。如果 ACT 分数提高 5 分,预期GPA 会提高多少? (Ⅱ)计算每次观测的拟合值和残差,并验证残差和(近似)为零。 (Ⅲ)当 20ACT 时,GPA 的预测值为多少? (Ⅳ)对这8 个学生来说,GPA 的变异中,有多少能由 ACT 解释?试说明。 答:(Ⅰ)变量的均值为:3.2125GPA , 25.875ACT 。 15.8125niiiGPAGPAACTACT 根据公式2.19 可得:1ˆ5.8125 / 56.8750.1022 。 根据公式2.17 可知:0ˆ3.21250.102225.8750.5681 。 因此0.56810.1022GPAACT^。此处截距没有一个很好的解释,因为对样本而言,ACT 并不接近0。如果ACT分数提高5 分,预期GPA 会提高0.1022×5=0.511。 (Ⅱ)每次观测的拟合值和残差表如表2-3 所示: 表2-3 i GPA GPA^ ˆu 1 2.8 2.7143 0.0857 2 3.4 3.0209 0.3791 3 3.0 3.2253 -0.2253 4 3.5 3.3275 0.1725 5 3.6 3.5319 0.0681 6 3.0 3.1231 -0.1231 7 2.7 3.1231 -0.4231 8 3.7 3.6341 0.0659 根据表可知,残差和为-0.002,忽略固有的舍入误差,残差和近似为零。 (Ⅲ)当 20ACT ,则0.56810.1022202.61GPA ^。 (Ⅳ)残差平...