传感器及检测技术例题集

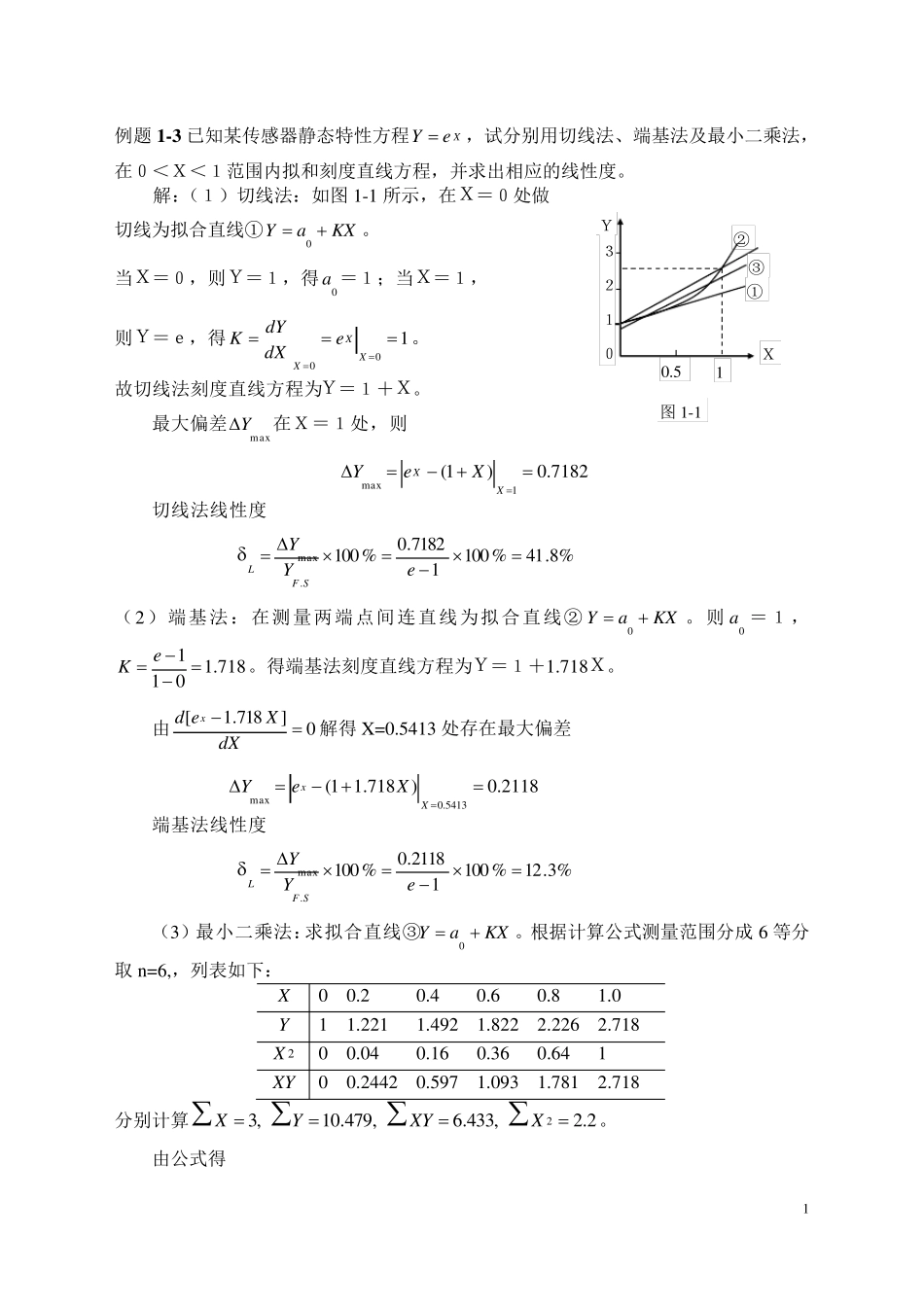
1 例题1 -3 已知某传感器静态特性方程XeY ，试分别用切线法、端基法及最小二乘法，在０＜Ｘ＜１范围内拟和刻度直线方程，并求出相应的线性度。 解：（１）切线法：如图1-1 所示，在Ｘ＝０处做 切线为拟合直线①KXaY0。 当Ｘ＝０，则Ｙ＝１，得0a ＝１；当Ｘ＝１， 则Ｙ＝ｅ，得100XXXedXdYK。 故切线法刻度直线方程为Ｙ＝１＋Ｘ。 最大偏差maxY在Ｘ＝１处，则 7182.0)1(1maxXXXeY 切线法线性度 %8.41%10017182.0%100.maxeYYSFL （2）端基法：在测量两端点间连直线为拟合直线②KXaY0。则0a ＝１，718.1011  eK。得端基法刻度直线方程为Ｙ＝１＋1.718Ｘ。 由0]718.1[dXXedx解得 X=0.5413 处存在最大偏差 2118.0)718.11(5413.0maxXxXeY 端基法线性度 %3.12%10012118.0%100.maxeYYSFL （3）最小二乘法：求拟合直线③KXaY0。根据计算公式测量范围分成 6 等分取 n=6,，列表如下： X 0 0.2 0.4 0.6 0.8 1.0 Y 1 1.221 1.492 1.822 2.226 2.718 X 2 0 0.04 0.16 0.36 0.64 1 XY 0 0.2442 0.597 1.093 1.781 2.718 分别计算2.2,433.6,479.10,32XXYYX。 由公式得 ② ① ３ ２ １ ０ Ｙ Ｘ 0.5 1 ③ 图1-1 2 ｌ U0 Ｒ１ Ｒ2 894.02.2632.2479.103433.6)(22220XnXXYXXYa 705.12.263433.66479.103)(222XnXYXnYXK 得最小二乘法拟合直线方程为Y=0.849+1.705X。 由0)705.1849.0(dXXedX解出X=0.5335。故 0987.0)705.1894.0(5335.0maxXxXeY 得最小二乘法线性度 %75.5%10010987.0eL 此题计算结果表明最小二乘法拟合的刻度直线L 值最小，因而此法拟合精度最高，在计算过程中若n取值愈大，则其拟合刻度直线L 值愈小。用三种方法拟合刻度直线如图1-1 所示①②③。 第二章电阻式传感器原理与应用 [例题分析] 例题2 -1 如果将100Ω电阻应变片贴在弹性试件上，若试件受力横截面积S = 0.5×10-4 m2，弹性模量 E =2×1011 N/m2 ，若有 F=5×104 N 的拉力引起应变电阻变化为1Ω。试求该应变片的灵敏度系数？ 解：由题意得应变片电阻相对变化量1001RR 根据材料力学理论可知：应变E（σ为试件所受应力，SF），故应变 00...