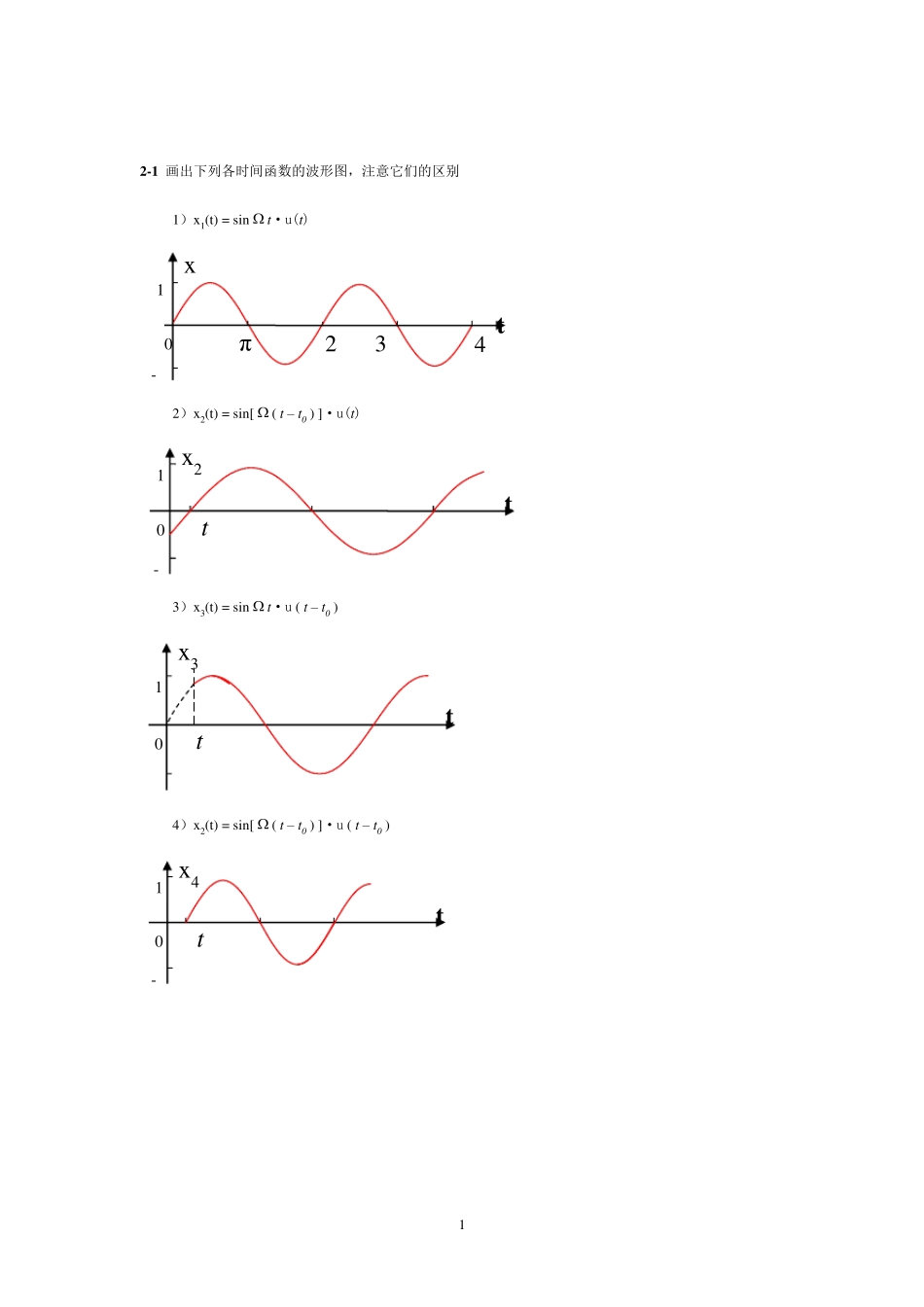
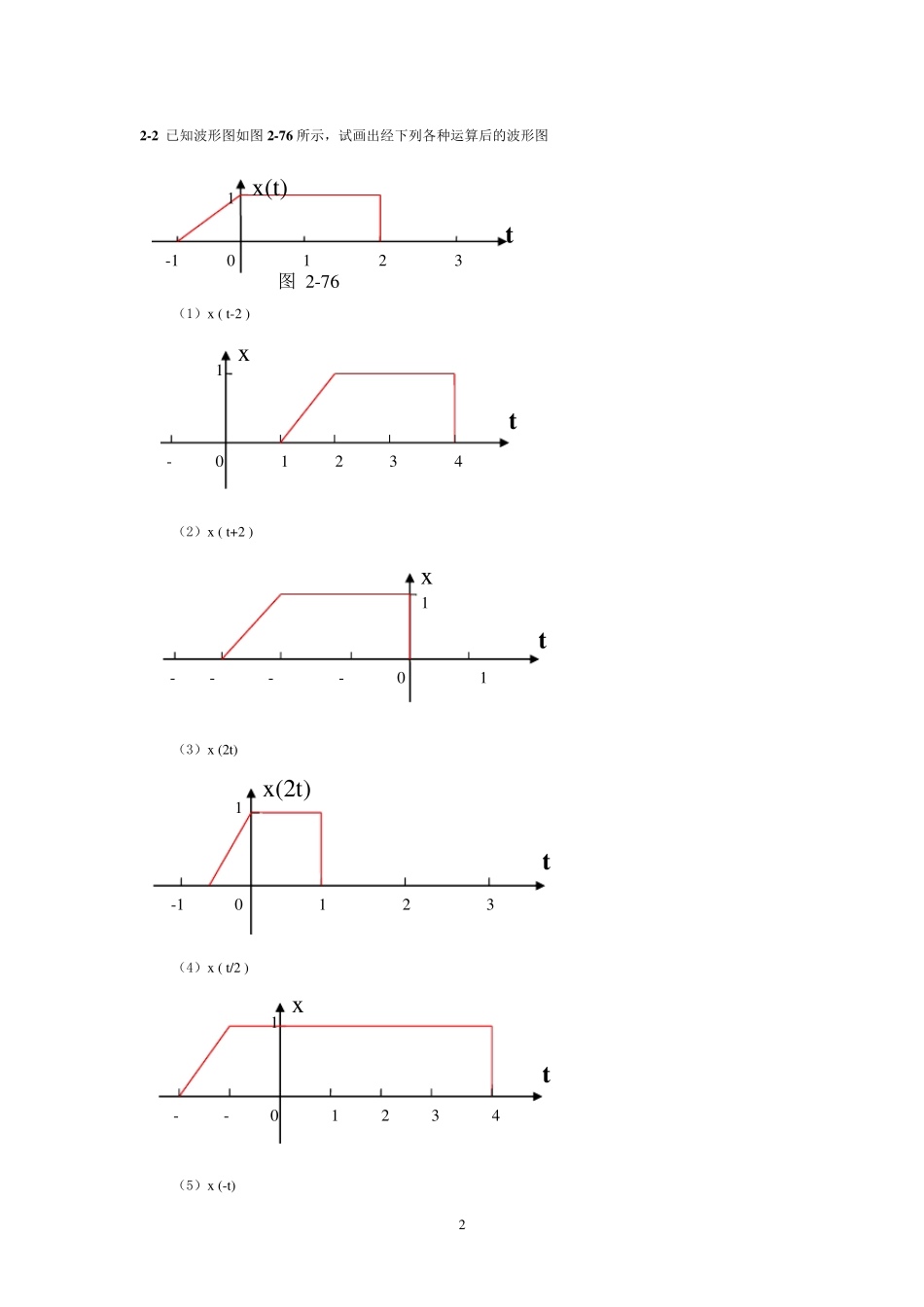
1 2-1 画出下列各时间函数的波形图,注意它们的区别 1)x 1(t) = sin t·u(t) 2)x 2(t) = sin[ ( t – t0 ) ]·u(t) 3)x 3(t) = sin t·u ( t – t0 ) 4)x 2(t) = sin[ ( t – t0 ) ]·u ( t – t0 ) 0 1 tt x 2-1 -π 23t x0 40 1 tt x 30 1 tt x 4- 2 2-2 已知波形图如图2-76 所示,试画出经下列各种运算后的波形图 (1)x ( t-2 ) (2)x ( t+2 ) (3)x (2t) (4)x ( t/2 ) (5)x (-t) 0 1 t x -1 2 3 4 -0 1 t x (t) -1 1 2 3 图 2-76 0 1 t x -1 2 3 4 0 1 t x (2t) -1 1 2 3 -1 t x ---0 1 3 (6)x (-t-2) (7)x ( -t/2-2 ) (8)dx /dt 2-3 应用脉冲函数的抽样特性,求下列表达式的函数值 (1) )(0ttxδ(t) dt = x (-t0) (2) )(0ttxδ(t) dt = x (t0) -3 1 t x (-t) 2 -2 -1 0 1 -1 t 0 ----1 -5 1 t 0 -4 -3 -2 -1 1 x ( -t/2-2 ) -7 -6 -8 0 1 t dx /dt -1 1 2 3 -2 -δ (t-2) x (-t-2) 4 (3))(0tt u(t - 20t) dt = u( 20t) (4) )(0tt u(t – 2t0) dt = u(-t0) (5) te tδ(t+2) dt = e2-2 (6)ttsinδ(t- 6) dt = 6+ 21 (7) dttttetj0 = dttetj –dtttetj)(0 = 1-0tje = 1 – cosΩt0 + jsinΩt0 2-4 求下列各函数 x 1(t)与 x 2(t) 之卷积,x 1(t)* x 2(t) (1) x1(t) = u(t), x2(t) = e-at · u(t) ( a>0 ) x1(t)* x2(t) =dtueua)()( = ta de0 = )1(1atea (2) x1(t) =δ(t+1) -δ(t-1) , x2(t) = cos(Ωt + 4) · u(t) x1(t)* x2(t) =dttut)]1()1([)]()4[cos( = cos[ Ω(t+1)+ 4]u(t+1) – cos[Ω(t-1)+ 4]u(t-1) (3) x1(t) = u(t) – u(t-1) , x2(t) = u(t) – u(t-2) x1(t)* x2(t) =dtutuuu)]1()()][2()([ 当 t <0 时,x1(t)* x2(t) = 0 当 0