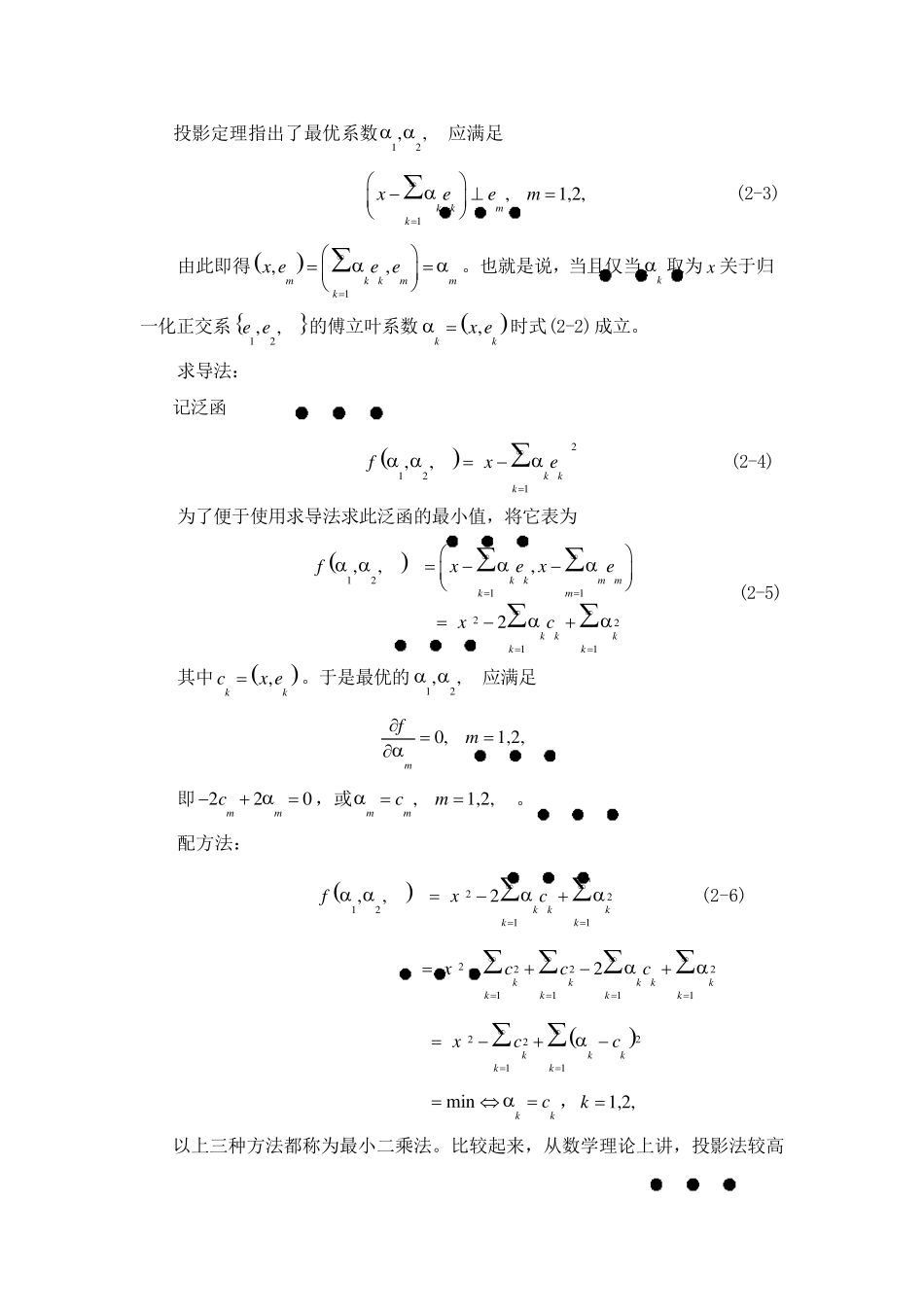
1、 叙 述 卡 享 南 —洛厄维变换,为什么该变换被称为最佳变换,何为其实用时的困难所在,举例说明其应用。 它 经 常 用 来 处 理 随 机 变 量 信 号 , 能 使 变 换 后 的 分 量 不 相 关 , 且 使 均 方 误 差 最小 , 所 以 常 称 作 最 佳 变 换 。 卡 享 南 -洛 厄 维 变 换 没 有 固 定 的 变 换 矩 阵 , 它 依 赖 于 给 定 的 随 机 向 量 的 协 方差 阵 。 正 是 这 种 变 换 的 特 点 , 也 是 它 在 实 际 使 用 时 的 困 难 所 在 , 因 为 它 需 要 依 照不 固 定 的 矩 阵xC 求 特 征 值 和 特 征 向 量 。 卡 享 南 -洛 厄 维 变 换 应 用 在 数 据 压 缩 技 术 中 。 特 别 是 随 着 信 息 时 代 的 发 展 到第 三 个 阶 段 -大 数 据 时 代 , 海 量 的 数 据 每 时 每 刻 扑 面 而 来 , 按 照 最 优 化 原 则 的 数据 压 缩 技 术 可 以 解 决 通 讯 和 数 据 传 输 系 统 的 信 道 容 量 不 足 问 题 。 通 过 对 信 号 作 正 交 变 换 , 根 据 失 真 最 小 的 原 则 在 变 换 域进行压 缩 。 卡 享 南 -洛 厄 维 变 换 使 这 种 变 换 消除了原 始信 号 诸分 量 间的 相 关 性,从而 使 数 据 压 缩 能 遵循均 方 误 差 最 小 的 准则 实 施。 2、最小二乘法的三种表现形式是什么?以傅里叶级数展开为例说明其各自的优缺点。 希尔伯特 空间中 线性逼近问 题 的 求 解 方 法称 为 最 小 二乘法。 它 有 三 种 不 同的表现形式:投影法、求 导法和 配方 法。 下面 以 傅里叶级数 展 开为 例来 说明。 投影法: 设 X 为 希尔伯特 空间, 12,,e e为 X 中 的 一组归一化 正 交 元素, x 为 X 中的 某一元素。 在 子空间12,,Mspan e e中 求 一元素0m , 使 得 0minm Mxmxm (2-1) 由于 M 中 的 元素可 表示为12,,e e的 线性组合, 那么问 题 就转化 为 求 系 数12,, , 使 得 1minkkkxe (2-2) 投影定理指出了最优系数12,, 应满足 1,1,2,kkmkxeem (2-3) 由此即...