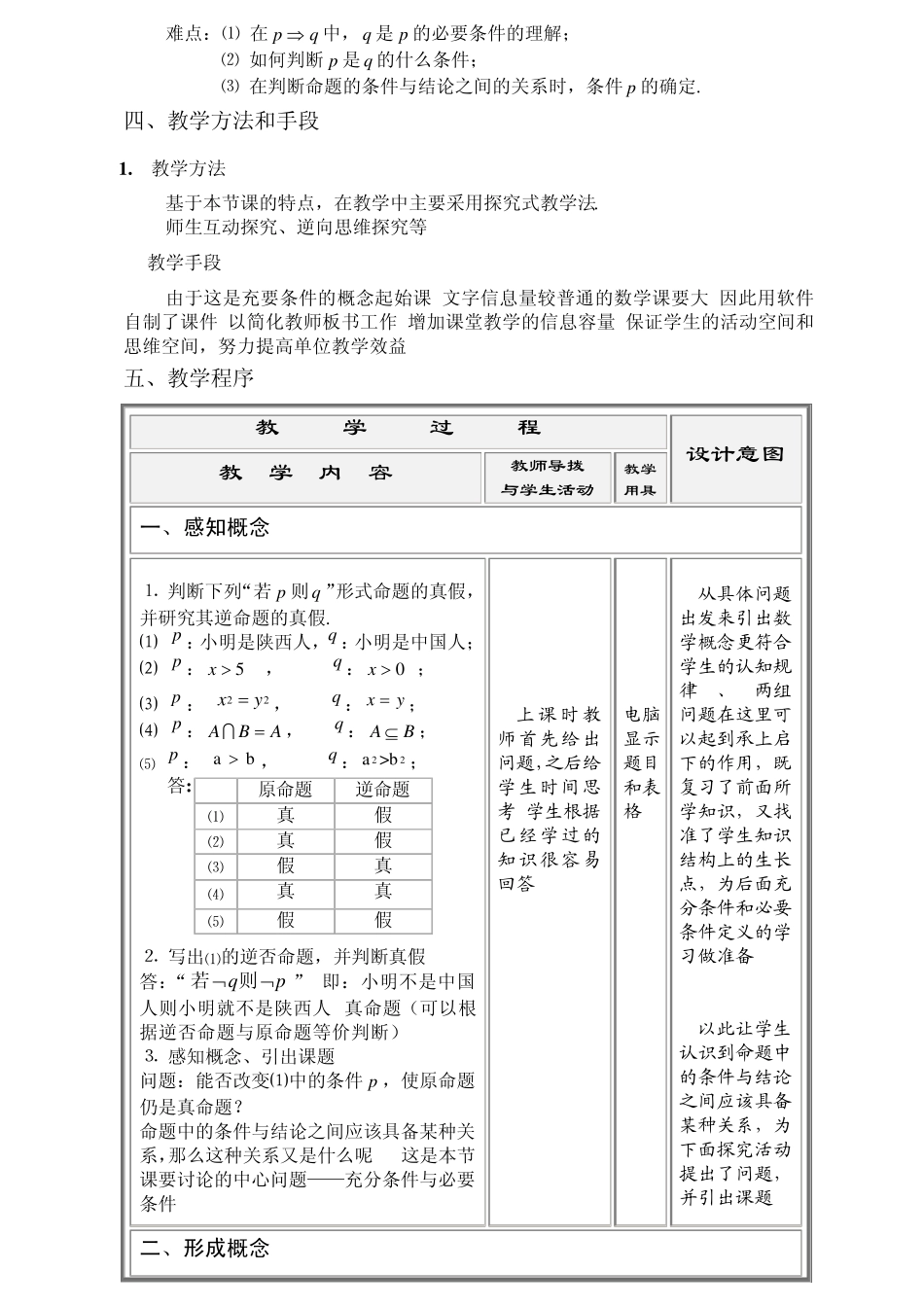
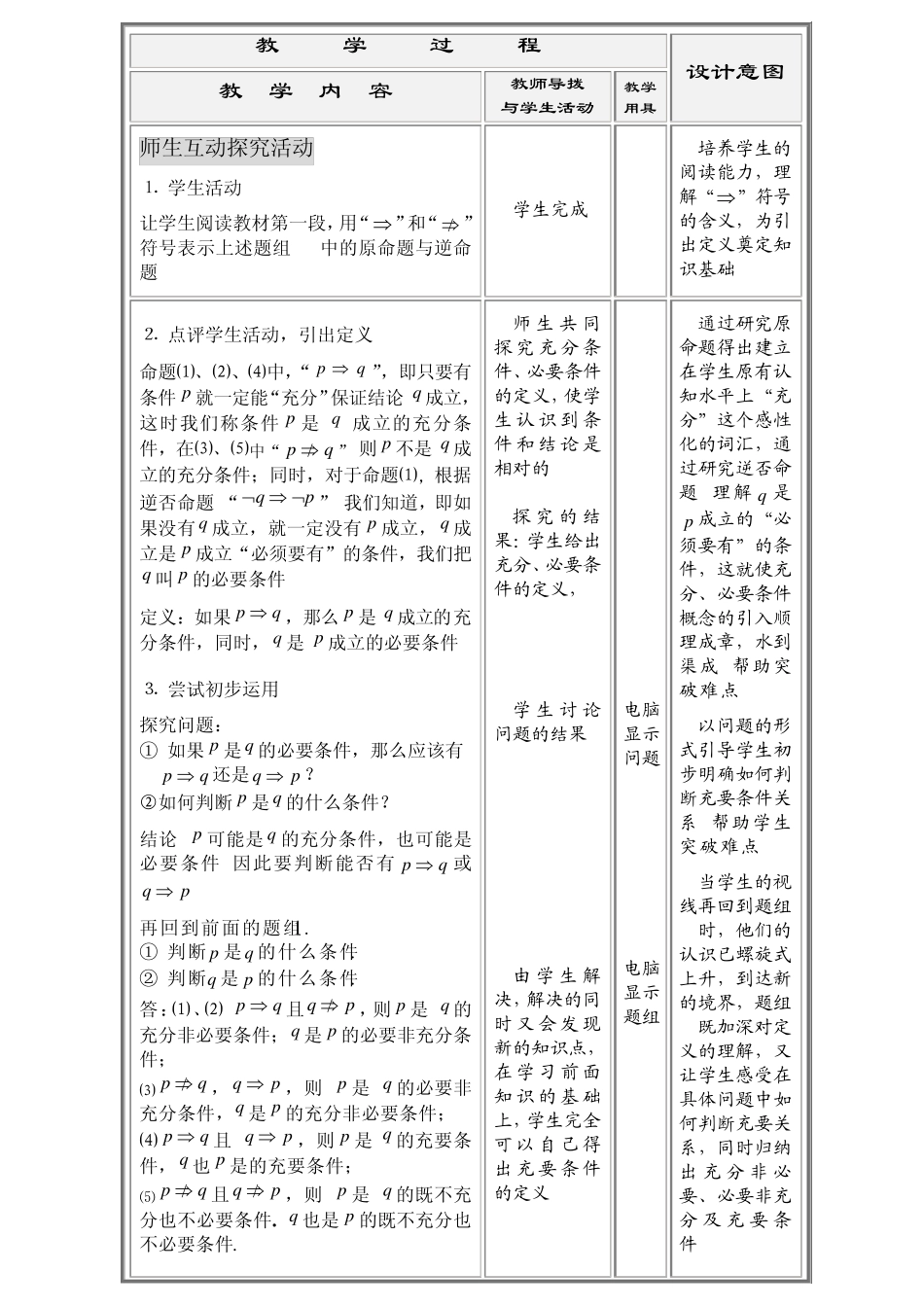
充分条件与必要条件 一、教案背景 1.面向学生:高中 学科:数学 2.课时:1 3.学生课前准备: (1)自学教材; (2)理解充分条件与必要条件的概念。 二、设计理念 著名教育学家布鲁纳说过:“知识的获得是一个主动过程. 学习者不应该是信息的被动接受者,而应是知识获取的主动参与者.”《数学课程标准》又提出数学教育要以有利于学生的全面发展为中心;以提供有价值的数学和倡导有意义的学习方式为基本点. 本节课的设计正是以此为理念,在整个授课过程中努力体现学生的主体地位,使学生亲自参与获取知识和技能的全过程,亲身体验知识的发生和发展过程,从而激发学生学习数学的兴趣,培养学生运用数学的意识和能力. 三、教材分析 1. 本节教材的地位、作用 数学活动离不开对问题进行等价转化与非等价转化, 充分条件、必要条件、充要条件及有关知识是进行这些转化的逻辑基础,它们是研究命题的条件与结论之间逻辑关系的重要工具,是中学数学中最重要的数学概念之一,虽然经过初中的学习,学生已经具备了一定的逻辑推理能力,但只有掌握了充分、必要条件的知识,并灵活运用它们进行推理判断,才可以说是建立起了保证数学活动顺利进行的完整的逻辑结构.为了提高这部分内容的学习质量, 教师在进行这一内容的教学时,不可拔高要求,追求一步到位,而要在今后的教学中滚动式逐步深化,使之与学生的知识结构同步发展、完善. 2.教学目标 ⑴ 知识与技能: 初步理解充分条件与必要条件以及充要条件的概念;基本掌握判断充要关系的方法与步骤. ⑵ 过程与方法: 从实例探究中感知概念;从原命题及逆否命题的对比分析中形成概念;从发散练习题的构造中理解概念;从集合的角度深化概念. ⑶ 情感、态度与价值观: 在对命题的条件与结论间逻辑关系的探究中培养学生思维的严谨性;在师生间平等、和谐的交流中,激发学生学习数学的热情. 3.教学重点、难点 本节课介绍了充分条件、必要条件和充要条件三个概念,这三个概念本身是重点.由于这些概念较抽象,与学生的原有思维习惯又有差异. 因此,对三个概念的理解以及运用它们解决相关问题也是本节内容的难点. 重点:⑴ 充分条件、必要条件、充要条件概念的理解; ⑵ 初步判断给定命题的条件与结论之间的关系. 难点:⑴ 在 pq中, q 是 p 的必要条件的理解; ⑵ 如何判断 p 是 q 的什么条件; ⑶ 在判断命题的条件与结论之间的关系时,条件 p 的确定. 四、教学方法和手段 ...