单整,协整,误差修正模型

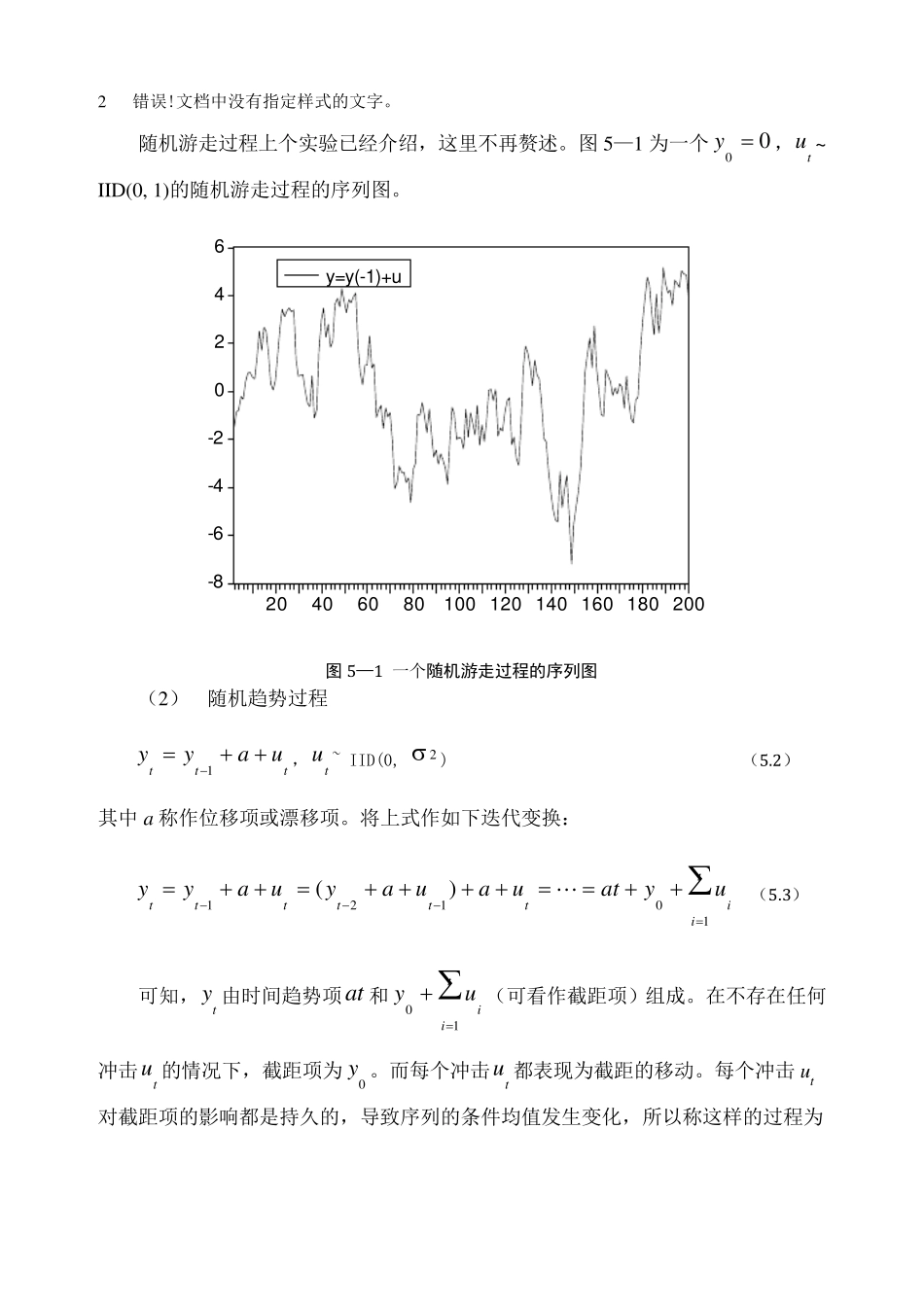
五 单位根检验、协整与误差修正模型 【实验目的与要求】 1 . 准确掌握单位根检验方程的形式和检验原理。 2 . 准确掌握单整、协整和误差修正模型的概念和形式。 3 . 学会利用单位根检验方法对样本序列进行协整关系检验。 4 . 熟练掌握运用误差修正模型对样本序列间的短期、长期关系进行分析。 5 . 在老师的指导下独立完成实验，得到正确的结果，并完成实验报告。 【实验准备知识】 在上个实验中，我们学习了如何运用相关分析图判断随机过程是否平稳，但这种方法比较粗略。检验随机过程是否平稳的一种比较正式的方法就是单位根检验。 在介绍单位根检验之前，我们有必要认识几种典型的非平稳随机过程。 1 . 几种典型的非平稳随机过程 （1 ） 随机游走过程 tttuyy1，tu ~ IID(0, 2) （5.1） 2 错误!文档中没有指定样式的文字。 随机游走过程上个实验已经介绍，这里不再赘述。图5—1 为一个00 y，tu ~ IID(0, 1)的随机游走过程的序列图。 -8-6-4-2024620406080100 120 140 160 180 200y=y(-1)+u 图5—1 一个随机游走过程的序列图 （2） 随机趋势过程 tttuayy1，tu ~ IID(0, 2) （5.2） 其中a 称作位移项或漂移项。将上式作如下迭代变换： tiittttttuyatuauayuayy10121)( （5.3） 可知，ty 由时间趋势项at 和tiiuy10（可看作截距项）组成。在不存在任何冲击tu 的情况下，截距项为0y 。而每个冲击tu 都表现为截距的移动。每个冲击 ut对截距项的影响都是持久的，导致序列的条件均值发生变化，所以称这样的过程为 随机趋势过程或有漂移项的随机游走过程。图5—2 为一个tttuyy3.01，00 y，tu ~ IID(0, 1)的随机趋势过程的序列图。 02040608010020406080100 120 140 160 180 200y=0.3+y(-1)+u 图5—2 一个随机趋势过程的序列图 图5—2 表明，虽然总趋势不变，但该过程围绕趋势项上下游动。由（5.3）式还可以看出，a 是时间趋势项的系数（原序列的增长速度）。a 为正时，趋势向上；a 为负时，趋势向下。 （3） 趋势非平稳过程 tttutayy1，tu ~ IID(0, 2) （5.4） 其中 a 称作位移项或漂移项， t 称作趋势项。可见，趋势非平稳过程是随机趋势和确定性趋势的混合随机过程。将上式作如下迭代变换： ttttttutautayutayy))1((121...