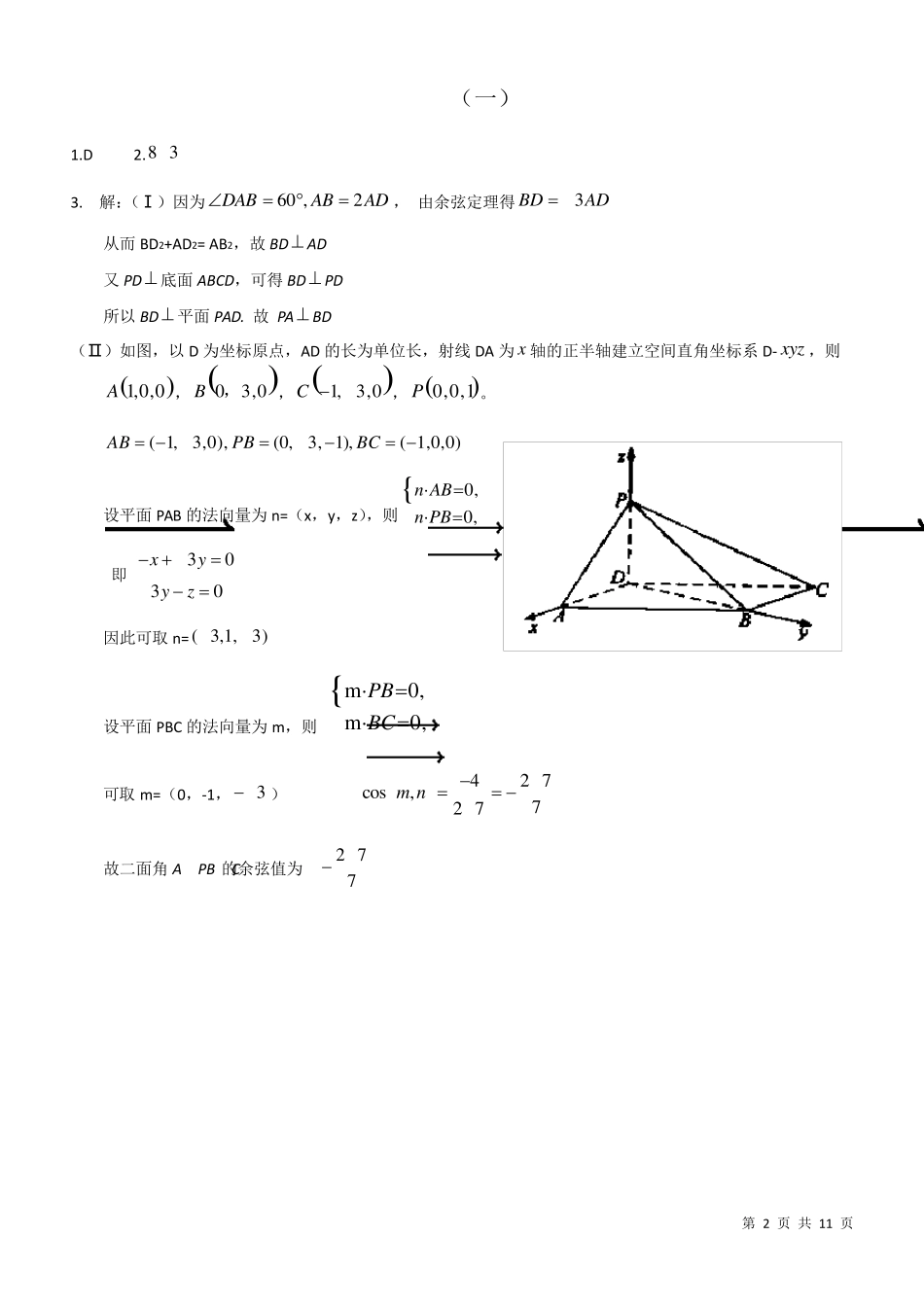
第 1 页 共 11 页 (一) 1 .在一个几何体的三视图中,正视图和俯视图如 右图所示,则相应的俯视图可以为 2.已知矩形ABCD 的顶点都在半径为4 的球O 的球面上,且6 ,23ABBC,则棱锥OABCD的体积为 。 3.如图,四棱锥P—ABCD 中,底面ABCD 为平行四 边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. (Ⅰ)证明:PA⊥BD; (Ⅱ)若 PD=AD,求二面角 A-PB-C 的余弦值。 第 2 页 共 11 页 (一) 1.D 2.8 3 3. 解:(Ⅰ)因为60 ,2DABABAD, 由余弦定理得 3BDAD 从而BD2+AD2= AB2,故BD AD 又PD 底面ABCD,可得BD PD 所以BD 平面PAD. 故 PA BD (Ⅱ)如图,以D 为坐标原点,AD 的长为单位长,射线DA 为x 轴的正半轴建立空间直角坐标系D- xyz ,则 1,0,0A,03,0B,,1, 3,0C ,0,0,1P。 ( 1,3,0),(0,3, 1),( 1,0,0)ABPBBC 设平面PAB 的法向量为n=(x,y,z),则0,0,{n ABn PB 即 3030xyyz 因此可取 n=( 3,1,3) 设平面PBC 的法向量为m,则 m0,m0,{PBBC 可取 m=(0,-1,3) 42 7cos,72 7m n 故二面角A-PB-C的余弦值为 2 77 第 3 页 共 11 页 (二) 1. 正方体ABCD-1111A B C D 中,B1B 与平面AC1D 所成角的余弦值为 A 23 B33 C 23 D63 2. 已知圆O 的半径为1,PA、PB 为该圆的两条切线,A、B 为俩切点,那么PA PB•的最小值为 (A) 42 (B) 32 (C) 42 2 (D) 32 2 3. 已知在半径为2 的球面上有A、B、C、D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为 (A) 2 33 (B) 4 33 (C) 2 3 (D) 8 33 4. 如图,四棱锥S-ABCD 中,SD 底面ABCD,AB//DC,AD DC,AB=AD=1,DC=SD=2,E 为棱SB 上的一点,平面EDC 平面SBC . (Ⅰ)证明:SE=2EB; (Ⅱ)求二面角A-DE-C 的大小 . 第 4 页 共 11 页 (二) 1. D 2. D 3. B 4. 解法一: (Ⅰ)连接 BD,取 DC 的中点 G,连接 BG, 由此知 1,DGGCBG即 ABC为直角三角形,故 BCBD. 又ABCD,BCSDSD 平面故, 所以, BC 平面BDS,BCDE . 作 BK EC,EDCSBCK为垂足,因平面平面, 故,BKEDCBKDE DE平面,与平面 SBC 内的两条相交直线 BK、BC 都垂直 DE⊥平面 SBC,DE⊥EC,DE...