原子物理学杨福家第三章题解

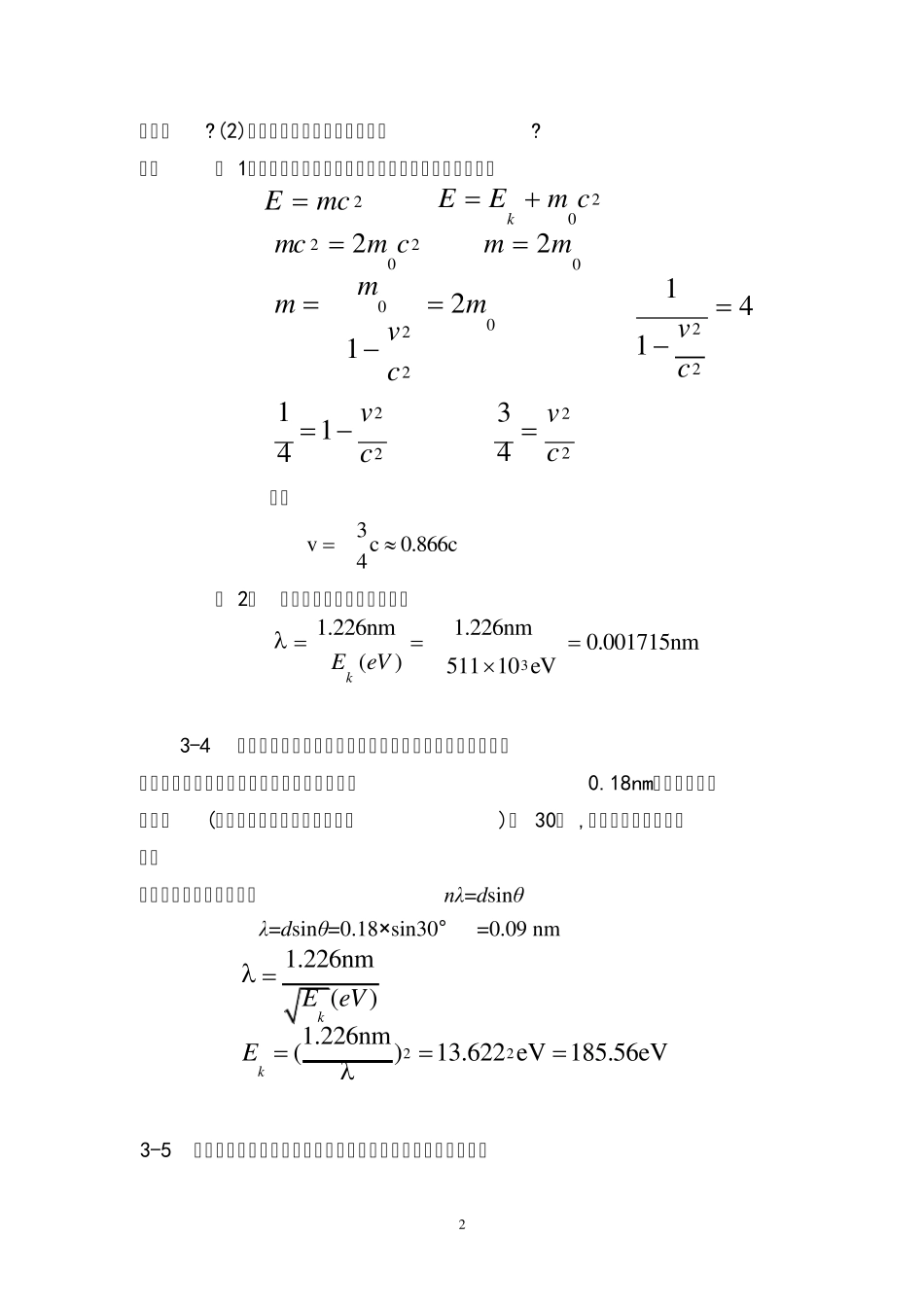
1 第 三 章 题 解 3-1 电 子 的 能 量 分 别 为 10eV， 100 eV， 1000 eV时 ， 试 计 算相 应 的 德 布 罗 意 波 长 。 解 ：依计 算 电 子 能 量 和电 子 波 长 对应 的 公式 电 子 的 能 量 : keekEmpmpE222 由德 布 罗 意 波 长 公式: KeEmhph2 nmE2 2 61 . nmnm3 8 801 01.1 .2 2 6 nmnm0 .1 2 2 61 0 01 .2 2 62 nmnm0 .0 3 8 81 0 0 01 .2 2 63 3-2 设光子 和电 子 的 波 长 均为 0.4nm， 试 问：（1）光子 的 动量 与电 子的 动量 之比是多少？ （2）光子 的 动能 与电 子 的 动能 之比是多少？ 解 ：（1）由ph可知光子 的 动量 等于电 子 的 动量 ， 即 p光子 :p电 子 =1:1 （2）由 光子 动能 与波 长 的 对应 的 关系 nmKeVE)(光子光子1 .2 4 电 子 动能 与波 长 的 关系 nmE电子电子1 .2 2 6 nmE2)(电子电子 1 .2 2 6 则知 962940..31 .2 2 61 01 .2 423电子光子EE 3-3 若一个电子的动能等于它的静止能量，试求：(1)该电子的速度 2 为多大?(2)其相应的德布罗意波长是多少? 解： （ 1）依题意，相对论给出的运动物体的动能表达式是： 2mcE  20cmEEk  2022cmmc 02mm  022021mcvmm 41122  cv 22141cv 2243cv 所以 0.866cc43v （ 2） 根据电子波长的计算公式： 0.001715nmeV105111.226nm)(1.226nm3eVEk 3-4 把热中子窄束射到晶体上，由布喇格衍射图样可以求得热中子的能量．若晶体的两相邻布喇格面间距为0.18nm，一级布喇格掠射角(入射束与布喇格面之间的夹角)为 30° ,试求这些热中子的能量． 解：根据布喇格衍射公式 nλ=dsinθ λ=dsinθ=0.18×sin30°nm=0.09 nm 1.226nm()kEeV  221.226nm()13.622 eV185.56eVkE 3-5 电子显微镜中所用加速电压一般都很高，电子被加速后的速度 3 很大，因而必须考虑相对论修正．试证明：电子的德布罗意波长与加速电压的关系应为： 1.226 nmrV  式中Vr=V(1+0.978× 10-6V)，称为相对论修正电压，其中电子加速电压 V 的单位是伏特． 分析:考虑德布罗意波长,考虑相对论情况质量能量修正,联系德布罗意关系式和相对论能量关系式,求出相对论下P 即可...