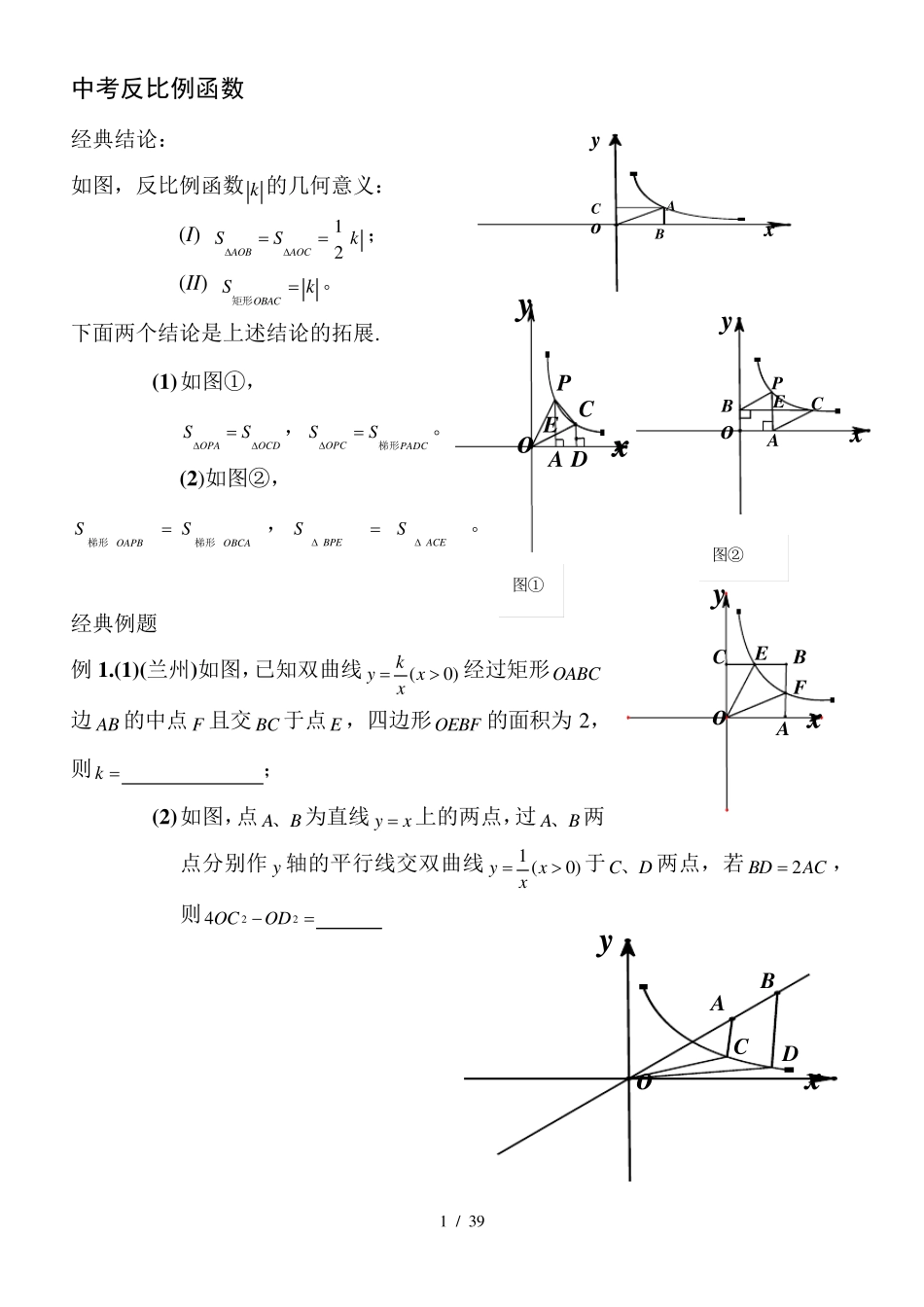
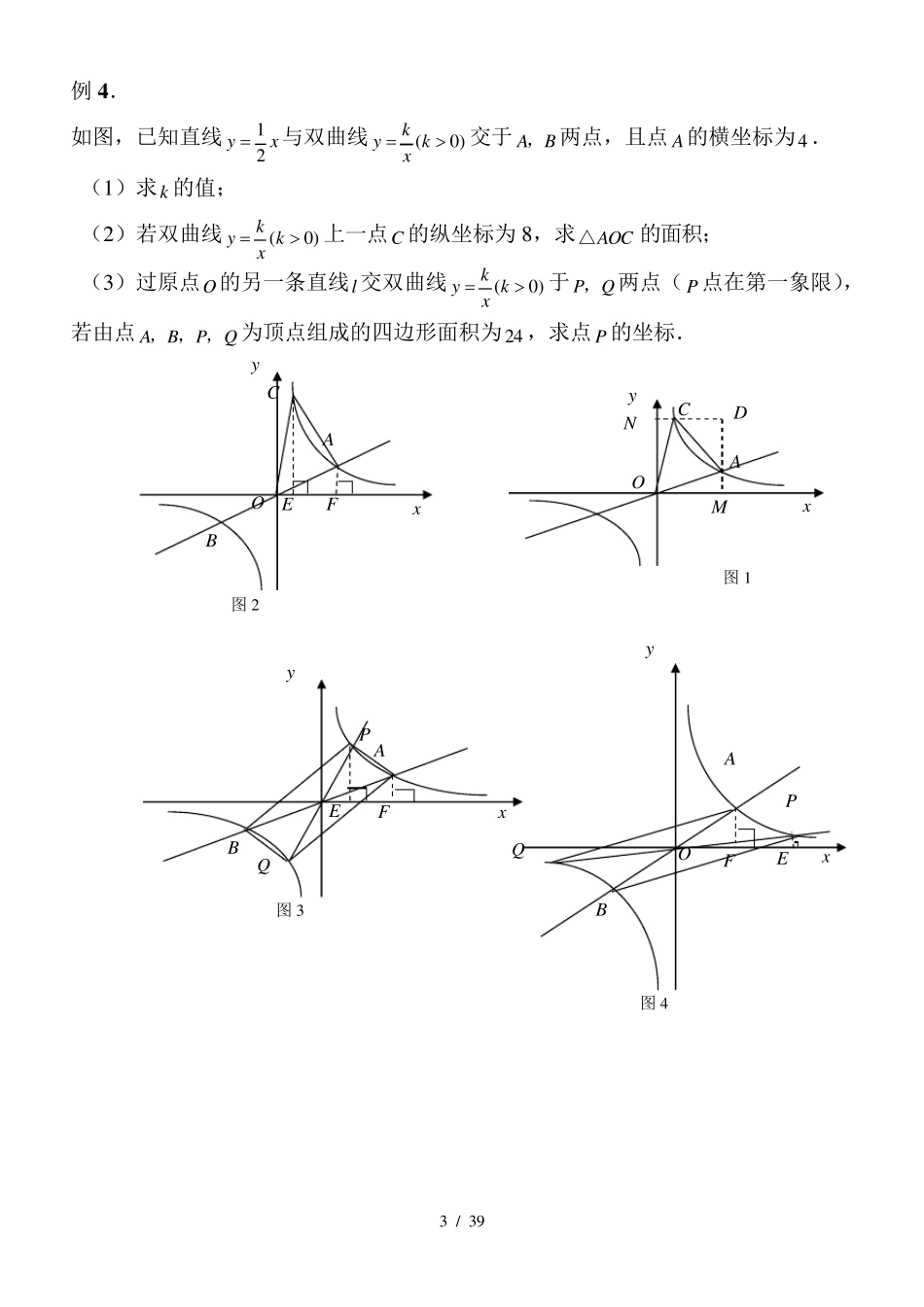
1 / 3 9 中考反比例函数 经典结论: 如图,反比例函数k 的几何意义: (I) 12AOBAOCSSk; (II) OBACSk矩形。 下面两个结论是上述结论的拓展. (1 ) 如图①, OPAOCDSS,OPCPADCSS梯形。 (2 )如图②, OAPBOBCASS梯形梯形,BPEACESS。 经典例题 例1 .(1 )(兰州)如图,已知双曲线(0 )kyxx经过矩形OABC边 AB 的中点 F 且交 BC 于点 E ,四边形OEBF 的面积为 2 ,则 k ; (2 ) 如图,点 AB、 为直线 yx 上的两点,过 AB、 两点分别作 y 轴的平行线交双曲线1 (0 )yxx于CD、 两点,若2BDAC,则224 OCOD FECBAoxyDCBAoxyCBAoyxEPDCAoyx图① EPCBAoyx图② 2 / 3 9 例2.如果一个正比例函数的图象与一个反比例函数xy6的图象交),(),,(2211yxByxA,那么))((1212yyxx值为 . 例3.如图,一次函数bkxy的图象与反比例函数xmy 的图象交于点A﹙-2 ,-5 ﹚,C﹙5 ,n﹚,交y 轴于点B,交x 轴于点D. (1 ) 求反比例函数xmy 和一次函数bkxy的表达式; (2 ) 连接OA,OC.求△AOC 的面积. O A B C x y D 3 / 3 9 例4 . 如图,已知直线12yx与双曲线(0 )kykx交于AB,两点,且点A的横坐标为4 . (1 )求k 的值; (2 )若双曲线(0 )kykx上一点C 的纵坐标为8 ,求AOC△的面积; (3 )过原点O的另一条直线l 交双曲线(0 )kykx于PQ,两点(P 点在第一象限),若由点ABPQ,,,为顶点组成的四边形面积为2 4 ,求点P 的坐标. 图2 O x A y B F E C 图3 A y B F Q E P x 图4 O x A y B F E Q P 图1 O x A y D M N C 4 / 3 9 例5 .(山东淄博) 如图,正方形AOCB 的边长为4 ,反比例函数的图象过点E(3 ,4 ). (1 )求反比例函数的解读式; (2 )反比例函数的图象与线段BC 交于点D,直线1yxb2过点D,与线段AB相交于点F,求点F 的坐标; (3 )连接OF,OE,探究∠AOF 与∠EOC 的数量关系,并证明. 。 (3 )∠AOF= 12∠EOC。 5 / 3 9 例6 .(2 0 0 9 山东威海)一次函数yaxb 的图象分别与x轴、y 轴交于点,M N ,与反比例函数kyx的图象相交于点,A B .过点A 分别作ACx轴,AEy轴,垂足分别为,C E ;过点B 分别作BFx轴,BDy轴,垂足分别为FD,,AC 与BD 交于点K ,连接CD....