哈工大传热学作业答案

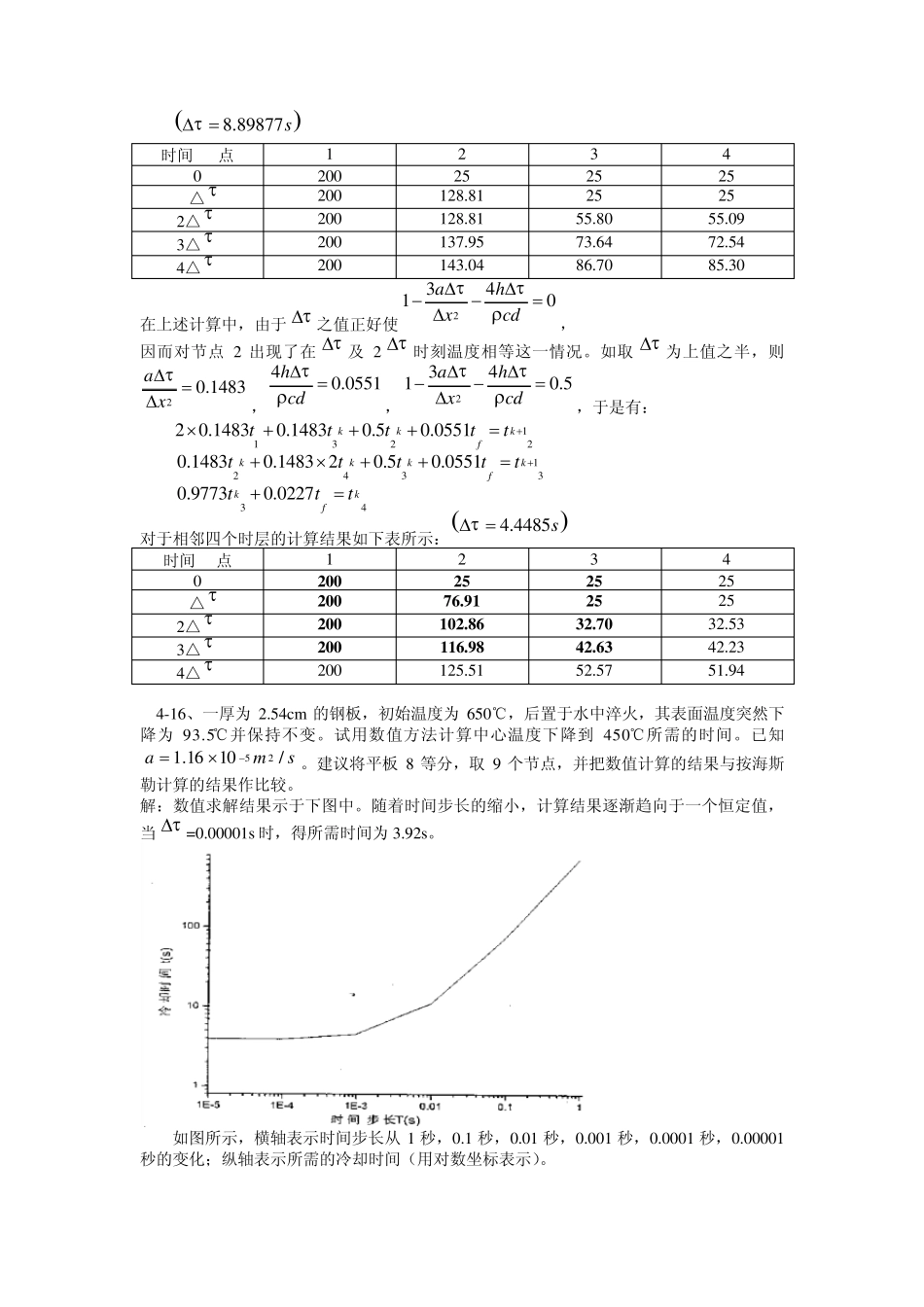
一维非稳态导热计算 4-15、一直径为1cm ,长4cm 的钢制圆柱形肋片，初始温度为25℃，其后，肋基温度突然升高到 200℃，同时温度为25℃的气流横向掠过该肋片，肋端及两侧的表面传热系数均为100。试将该肋片等分成两段（见附图），并用有限差分法显式格式计算从开始加热时刻起相邻 4 个时刻上的温度分布（以稳定性条件所允许的时间间隔计算依据）。已知＝43W/(m .K)，。（提示：节点 4的离散方程可按端面的对流散热与从节点 3 到节点 4 的导热相平衡这一条件列出）。 解：三个节点的离散方程为： 节点 2： 节点 3： 节点 4： 。 以上三式可化简为： 稳定性要求，即。 ，代入得： ， 如取此值为计算步长，则： ，。 于是以上三式化成为： )./(2 KmWsma/10333.125 12223212222/ 2444kkkkkkkfttttttdddd x h ttcxxx 12224323333/ 2444kkkkkkkfttttttdddd x h ttcxxx22344/ 244kkkfttddh ttx1213222243421kkfaahahtttttxxcdxcd1324322243421kkfaahahtttttxxcdxcd4322kkfx h ttx ht  23410ahxcd2341/ahxcd554332.258 101.333 10ca5253 1.333 104 10011/8.898770.020.01 32.258 100.099975 0.0124s 5221.333 108.898770.29660.02ax544 100 8.898770.110332.258 100.01hcd11322 0.29660.29660.1103kkftttt 12430.29660.296620.1103kkkftttt 340.97730.0227kkfttt 时间 点 1 2 3 4 0 200 25 25 25 △ 200 128.81 25 25 2△ 200 128.81 55.80 55.09 3△ 200 137.95 73.64 72.54 4△ 200 143.04 86.70 85.30 在上述计算中，由于之值正好使， 因而对节点2 出现了在及2时刻温度相等这一情况。如取为上值之半，...