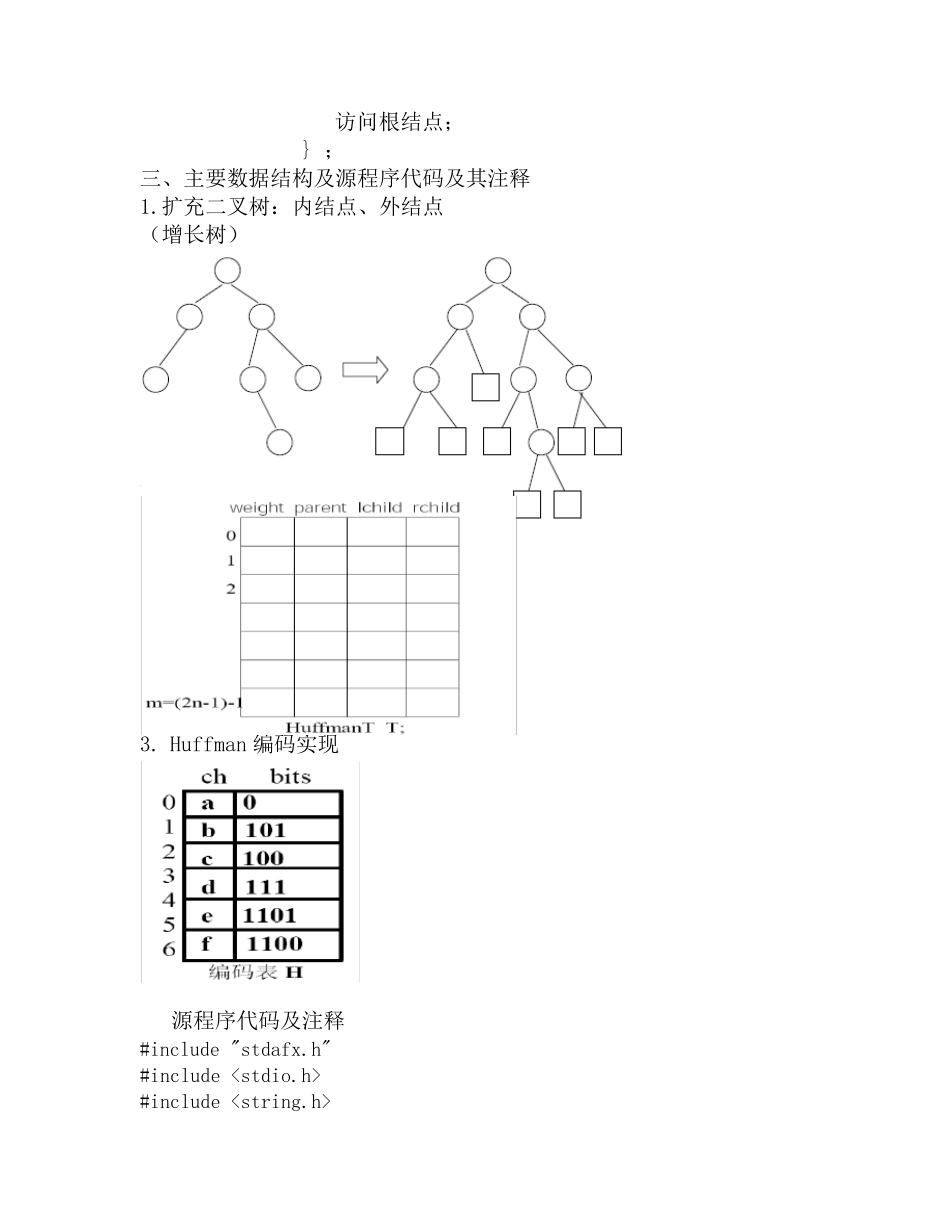
一、 问题描述 1. 用户输入字母及其对应的权值,生成哈夫曼树; 2. 通过最优编码的算法实现,生成字母对应的最优0、1 编码; 3. 先序、中序、后序遍历哈夫曼树,并打印其权值。 二、 方法思路 1.哈夫曼树算法的实现 §存储结构定义 #define n 100 /* 叶子树*/ #define m 2*(n) –1 /* 结点总数*/ typedef struct { /* 结点型*/ double weight ; /* 权值*/ int lchild ; /* 左孩子链*/ int rchild ; /* 右孩子链*/ int parent; /* 双亲链*/ 优点? }HTNODE ; typedef HTNODE HuffmanT[ m ] ; /* huffman 树的静态三叉链表表示*/ 算法要点 1)初始化:将 T[0],…T[m-1]共 2n-1 个结点的三个链域均置空( -1 ),权值为 0; 2)输入权值:读入n 个叶子的权值存于 T 的前 n 个单元 T[0],…T[n], 它们是 n 个独立的根结点上的权值; 3)合并:对森林中的二元树进行 n-1 次合并,所产生的新结点 依次存放在 T[i](n<=i<=m-1)。每次合并分两步: (1) 在当前森林中的二元树T [0],…T[i-1]所有结点中选取权值 最小和次最小的两个根结点 T[p1]和 T[p2]作为合并对象,这 里 0<= p1,p2<= i –1; (2) 将根为 T[p1]和 T[p2]的两株二元树作为左、右子树合并为一 株新二元树,新二元树的根结点为 T[i]。即 T[p1].parent =T[p2].parent = i ,T[i].lchild= p1, T[i].rchild=p2, T[i].weight =T[p1].weight + T[p2].weight。 2. 用huffman 算法求字符集最优编码的算法: 1) 使字符集中的每个字符对应一株只有叶结点的二叉树,叶的权值为对应字符的使用频率; 2) 利用huffman 算法来构造一株huffman 树; 3) 对huffman 树上的每个结点,左支附以0,右支附以1(或者相反),则从根到叶的路上的0、1 序列就是相应字符的编码 Huffman 编码实现: 存储结构 typedef struct{ char ch; //存储字符 char bits[n+1]; //字符编码位串 }CodeNode; typedef CodeNode HuffmanCode[n]; HuffmanCode H; 3. 二叉树遍历的递归定义 先根顺序遍历二叉树: 若二叉树非空则: { 访问根结点; 先根顺序遍历左子树; 先根顺序遍历右子树; } 中根顺序遍历二叉树: 若二叉树非空则: { 中根顺序遍历左子树; 访问根结点; 中根顺序遍历右子树; } 后根顺序遍历二叉树: 若二叉树非空则: { 后根顺序遍历左子树; 后根顺序遍...