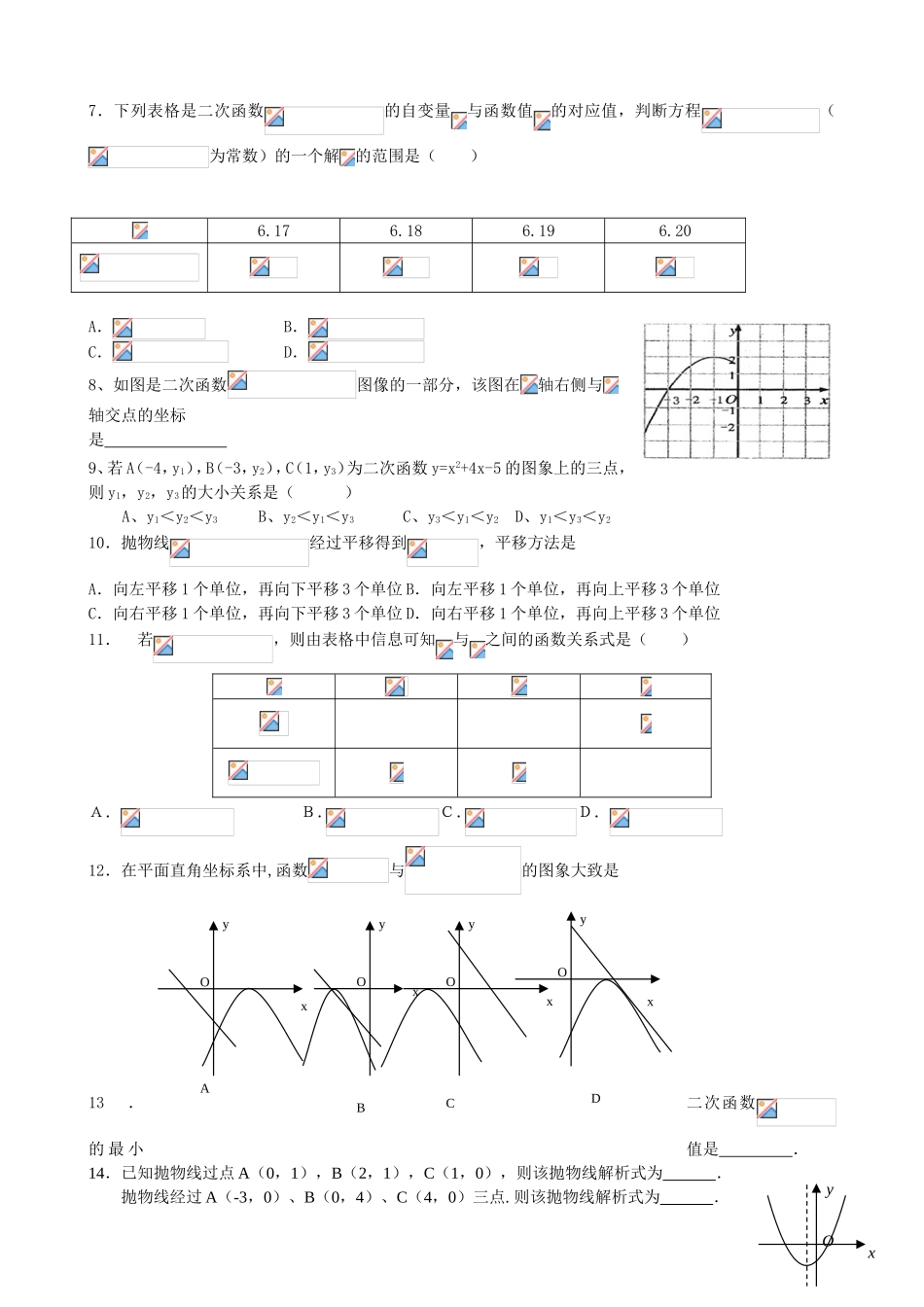
课题:《二次函数》小结与复习(第一课时)【复习目标】1.了解二次函数的表示方法.抛物线的开口方向、顶点坐标、对称轴以及抛物线与对称轴的交点坐标等.3.一元二次方程与抛物线的结合与应用.活动1:知识梳理1.二次函数解析式的三种表示方法:(1)顶点式:(2)交点式:(3)一般式:2.填表:抛物线对称轴顶点坐标开口方向y=ax2当a>0时,开口当a<0时,开口y=ax2+ky=a(x-h)2y=a(x-h)2+ky=ax2+bx+c3.二次函数y=ax2+bx+c,当a>0时,在对称轴右侧,y随x的增大而,在对称轴左侧,y随x的增大而;当a<0时,在对称轴右侧,y随x的增大而,在对称轴左侧,y随x的增大而4.抛物线y=ax2+bx+c,当a>0时图象有最点,此时函数有最值;当a<0时图象有最点,此时函数有最值活动2:探究、讨论、练习1.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时,x的取值范围是A.-1<x<3B.x>3C.x<-1D.x>3或x<-12.已知二次函数()的图象如图5所示,有下列4个结论:①;②;③;④;其中正确的结论有()A.1个B.2个C.3个D.4个3.已知抛物线y=3x2上有一点的横坐标为2,则该点的纵坐标为.4.已知二次函数y=3x2-5有一点的纵坐标是2,则该点横坐标为__________.5.对于抛物线,下列说法正确的是()A.开口向下,顶点坐标B.开口向上,顶点坐标C.开口向下,顶点坐标D.开口向上,顶点坐标6.在同一直角坐标系中,函数和(是常数,且)的图象可能是()-1Ox=1yxxyOA.xyOB.xyOC.xyOD.xDxOyAyxOByxOOyC7.下列表格是二次函数的自变量与函数值的对应值,判断方程(为常数)的一个解的范围是()6.176.186.196.20A.B.C.D.8、如图是二次函数图像的一部分,该图在轴右侧与轴交点的坐标是9、若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是()A、y1<y2<y3B、y2<y1<y3C、y3<y1<y2D、y1<y3<y210.抛物线经过平移得到,平移方法是A.向左平移1个单位,再向下平移3个单位B.向左平移1个单位,再向上平移3个单位C.向右平移1个单位,再向下平移3个单位D.向右平移1个单位,再向上平移3个单位11.若,则由表格中信息可知与之间的函数关系式是()A.B.C.D.12.在平面直角坐标系中,函数与的图象大致是13.二次函数的最小值是.14.已知抛物线过点A(0,1),B(2,1),C(1,0),则该抛物线解析式为.抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.则该抛物线解析式为.Oxy15.抛物线与x轴只有一个公共点,则m的值为.16.二次函数图象如图所示,则点在第象限.17.已知二次函数的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数的图象上,则下列结论正确的是A.y1<y2<y3B.y2<y1<y3C.y3<y1<y2D.y1<y3<y218.已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)①求该函数的关系式;②求该函数图象与坐标轴的交点坐标;③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△OA′B′的面积.19.如图,直线和抛物线都经过点A(1,0),B(3,2).⑴求m的值和抛物线的解析式;⑵求不等式的解集(直接写出答案).20.如图,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0)。(1)求抛物线的解析式及顶点D的坐标;(4分)(2)判断△ABC的形状,证明你的结论;(4分)(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.(4分)21.已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别相交于点A(-1,0)、B(0,3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.22.如图20,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,直线m运动的时间为t(秒).(1)点A的坐标是__________,点C的坐标是__________;(2)当t=秒或秒时,MN=AC;(3)设△OMN的面积为S,求S与t的函数关系式;(4)探求(3)中得到的函数S有没有最大值?若有,求出最大值;若没有,要说明理由.图20