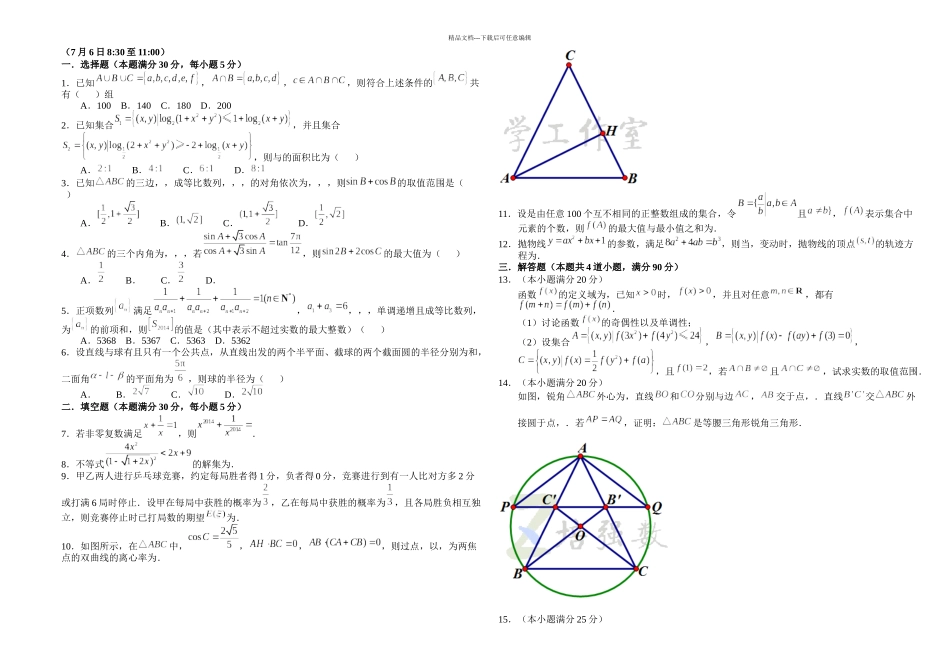
精品文档---下载后可任意编辑(7 月 6 日 8:30 至 11:00)一.选择题(本题满分 30 分,每小题 5 分)1.已知,,,则符合上述条件的共有( )组A.100 B.140 C.180 D.2002.已知集合,并且集合,则与的面积比为( )A. B. C. D.3.已知的三边,,成等比数列,,,的对角依次为,,,则的取值范围是( )A. B. C. D.4.的三个内角为,,,若,则的最大值为( )A. B. C. D.5.正项数列满足,,,,单调递增且成等比数列,为的前项和,则的值是(其中表示不超过实数的最大整数)( )A.5368 B.5367 C.5363 D.53626.设直线与球有且只有一个公共点,从直线出发的两个半平面、截球的两个截面圆的半径分别为和,二面角的平面角为,则球的半径为( )A. B. C. D.二.填空题(本题满分 30 分,每小题 5 分)7.若非零复数满足,则.8.不等式的解集为.9.甲乙两人进行乒乓球竞赛,约定每局胜者得 1 分,负者得 0 分,竞赛进行到有一人比对方多 2 分或打满 6 局时停止.设甲在每局中获胜的概率为,乙在每局中获胜的概率为,且各局胜负相互独立,则竞赛停止时已打局数的期望为.10.如图所示,在中,,,,则过点,以,为两焦点的双曲线的离心率为.11.设是由任意 100 个互不相同的正整数组成的集合,令且,表示集合中元素的个数,则的最大值与最小值之和为.12.抛物线的参数,满足,则当,变动时,抛物线的顶点的轨迹方程为.三.解答题(本题共 4 道小题,满分 90 分)13.(本小题满分 20 分)函数的定义域为,已知时,,并且对任意,都有.(1)讨论函数的奇偶性以及单调性;(2)设集合,,,且,若且,试求实数的取值范围.14.(本小题满分 20 分)如图,锐角外心为,直线和分别与边,交于点,.直线交外接圆于点,.若,证明:是等腰三角形锐角三角形.15.(本小题满分 25 分)精品文档---下载后可任意编辑已知数列中,,对于任意的,有.(1)求数列的通项公式;(2)数列满足,求数列的通项公式;(3)设,是否存在实数,当时,恒成立,若存在,求实数的取值范围;若不存在,请说明理由.16.(本小题满分 25 分)已知抛物线,直线与抛物线相交于,两点,连结及抛物线顶点的直线交准线于,连结及的直线交准线于,并且与都平行于轴.(1)证明:直线过定点;(2)求四边形的面积的最小值.2024 年全国高中数学联赛辽宁省初赛试题及参考答案及评分标准说...