分子量及其分布复习题答案

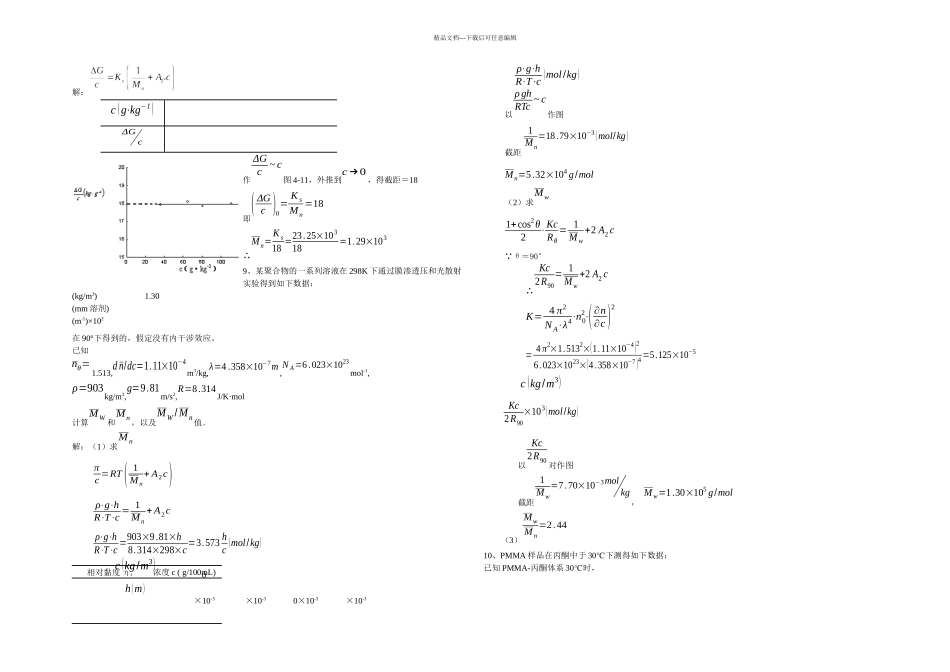
02468101230405060708090 c×103g/mLcd精品文档---下载后可任意编辑1、假定 A 与 B 两聚合物试样中都含有三个组分，其相对分子质量分别为 1 万、10 万和 20 万，相应的重量分数分别为：A 是 0.3、0.4 和 0.3，B 是 0.1、0.8 和 0.1，计算此二试样的M n 、M w 和M z，并求其分布宽度指数、和多分散系数 d。解：（1）对于 AM n=1∑W iM i=10.3104 + 0.4105 +0.32×105=28169Mw=∑W iMi=0.3×104+0.4×105+0.3×2×105=103000M z=∑ W iM i2M w=0.3×108+0.4×1010+0.3×4×1010103000=155630d=M w/M n=3.66σ n2=Mn2 (d−1)=281692×3.66=2.90×109σ w2=Mw2 (d−1)=1030002×3.66=3.88×1010（2）对于 BM n=54054M w=101000M z=118910d=1.87σ n2=2.54×109σ w2 =8.87×1092、用醇酸缩聚法制得的聚酯，每个分子中有一个可分析的羧基，现滴定的聚酯用去 0.1N 的 NaOH 溶液 0.75毫升，试求聚酯的数均相对分子质量。解：聚酯的摩尔数为0.75×10−3 L×0.1mol/L=7.5×10−5molM n=1.5 g7.5×10−5mol=2×104 g/mol3、某沸点升高仪采纳热敏电阻测定温差 ΔT，检流计读数 Δd 与 ΔT 成正比。用苯作溶剂，三硬脂酸甘油酯（M=892 克×10－3g/mL，测得 Δd 为 786。今用此仪器和溶剂测聚二甲基硅氧烷的相对分子质量，浓度和 Δd的关系如下表：c×103g/mL00Δd3115277158731109试计算此试样的相对分子质量。解：（1）标定时，ΔT =K' cM 已知Δd=786 c=1.2×10−3g/mL 即Δd=K cM M=892∴K= Δd⋅Mc=786×8921.2×10−3 =58426×104 （2）测定时，(ΔTc )c→0=K 'M 即 (Δdc )c→0= KM 以Δdc对作图，外推到c=0c×103g/mL00Δd/c ×10-3从图 4-3 得(Δdc )c→0= KM =36.78×103∴M n=58426×10436×103=162294、于 25℃，测定不同浓度的聚苯乙烯-甲苯溶液的渗透压，结果如下：c×103（g/cm3）00渗透压（g/cm2）0试求此聚苯乙烯的数均相对分子质量、第二维里系数 A2和 Huggins 参数1。已知 ρ（甲苯）＝/毫升，ρ（聚苯乙烯）＝/毫升。解：πc =RT(1M + A2 c) 以πc对作图或用最小二乘法求得πc ×10−3( cm)1234567890.060.080.100.120.140.160.180.20c×103 （ g/cm3 ）)(10 3cmc0246880100120140160180 c2133cVVRTc2133cVVRTc精品文档---下载后可任...