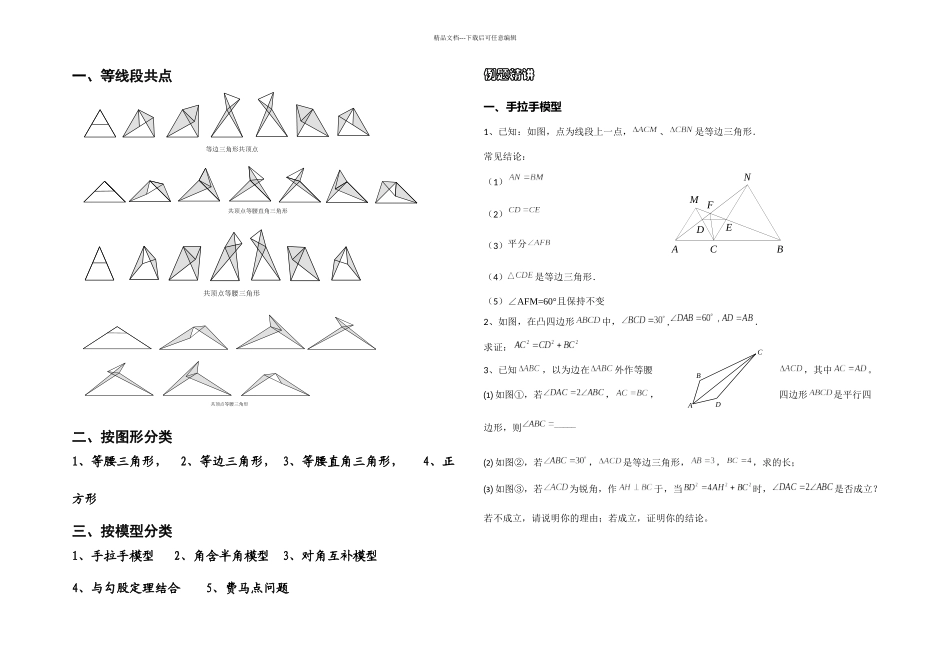
MDNECBFAABCD精品文档---下载后可任意编辑一、等线段共点二、按图形分类1、等腰三角形, 2、等边三角形, 3、等腰直角三角形, 4、正方形三、按模型分类1、手拉手模型 2、角含半角模型 3、对角互补模型 4、与勾股定理结合 5、费马点问题例题精讲一、手拉手模型1、已知:如图,点为线段上一点,、是等边三角形.常见结论:(1)(2)(3)平分(4)是等边三角形.(5)∠AFM=60°且保持不变2、如图,在凸四边形中,,.求证:3、已知,以为边在外作等腰,其中。⑴ 如图①,若,,四边形是平行四边形,则⑵ 如图②,若,是等边三角形,,,求的长;⑶ 如图③,若为锐角,作于,当时,是否成立?若不成立,请说明你的理由;若成立,证明你的结论。等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形精品文档---下载后可任意编辑二、角含半角模型4、已知:如图 1 在中,,,点、分别为线段上两动点,若.探究线段、、三条线段之间的数量关系.小明的思路是:把绕点顺时针旋转,得到,连结,使问题得到解决.请你参考小明的思路探究并解决下列问题:⑴ 猜想、、三条线段之间存在的数量关系式,并对你的猜想给予证明; ⑵ 当动点在线段上,动点运动在线段延长线上时,如图 2,其它条件不变,⑴中探究的结论是否发生改变?说明你的猜想并给予证明.5、在正方形 ABCD 中,点 E、F 分别在边 BC、CD 上,且∠EAF=CEF=45°∠,(1)将△ADF 绕着点 A 顺时针旋转 90°,得到△ABG,如图 1,求证:△AEGAEF≌△;(2)若直线 EF 与 AB、AD 的延长线分别交于点 M,N,如图 2,求证:(3)将正方形改为长与宽不相等的矩形,若其余条件不变,请你直接写出线段 EF,BE,DF之间的数量关系。6、在等边Δ ABC的两边 AB,AC 所在直线上分别有两点 M,N,D 为Δ ABC外一点,且∠ MDN=60°,∠BDC=120° ,BD=CD,探究:当点 M,N 分别爱直线 AB,AC 上移动时,BM,NC,MN 之间的数量关系及Δ AMN 的周长与等边Δ ABC的周长 L 的关系.⑴ 如图①,当点 M,N 在边 AB,AC 上,且 DM=DN 时,BM,NC,MN 之间的数量关系式__________;此时QL =__________⑵ 如图②,当点 M,N 在边 AB,AC 上,且DM≠DN 时,猜想(1)问的两个结论还成立吗?写出你的猜想并加以证明;⑶ 如图③,当点 M,N 分别在边 AB,CA 的延长线上时,若 AN=x,则 Q=_________(用 x,L表示)图(1) 图(2)...