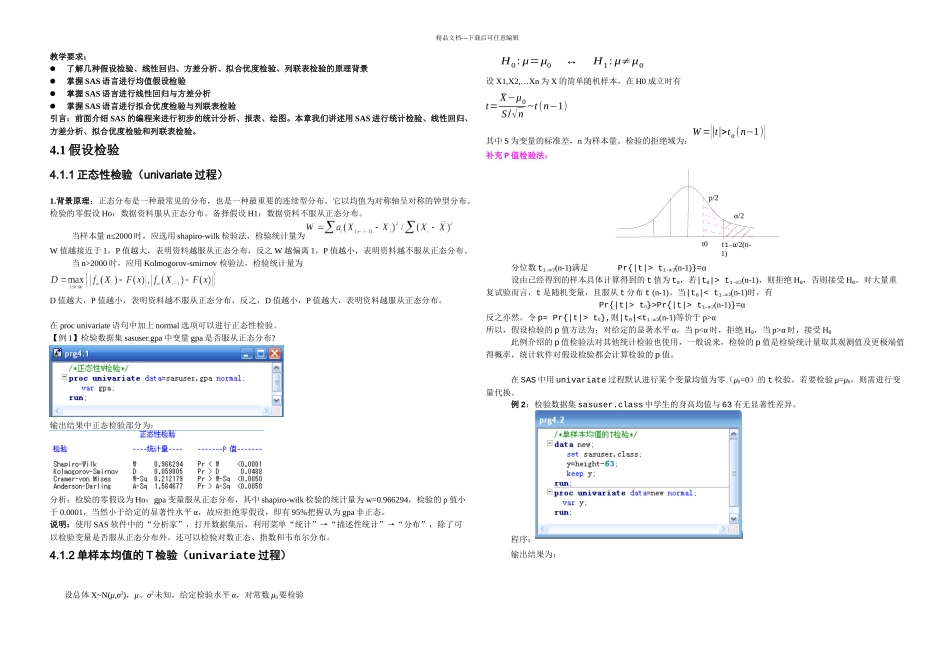
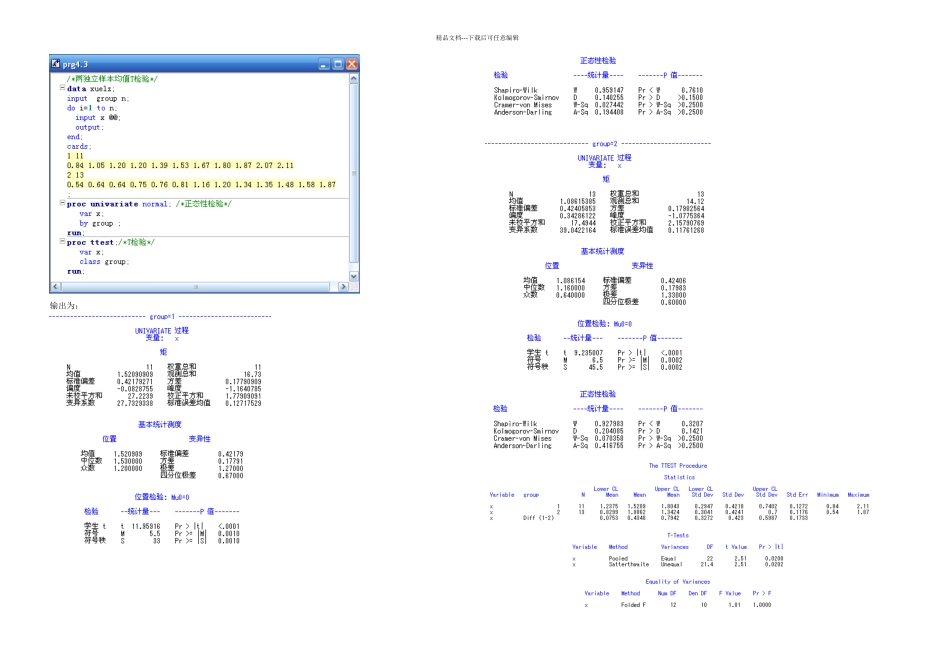
t1-α/2(n-1)α/2t0p/2精品文档---下载后可任意编辑教学要求:了解几种假设检验、线性回归、方差分析、拟合优度检验、列联表检验的原理背景掌握 SAS 语言进行均值假设检验掌握 SAS 语言进行线性回归与方差分析掌握 SAS 语言进行拟合优度检验与列联表检验引言:前面介绍 SAS 的编程来进行初步的统计分析、报表、绘图。本章我们讲述用 SAS 进行统计检验、线性回归、方差分析、拟合优度检验和列联表检验。4.1 假设检验4.1.1 正态性检验(univariate 过程)1.背景原理:正态分布是一种最常见的分布,也是一种最重要的连续型分布,它以均值为对称轴呈对称的钟型分布。检验的零假设 Ho:数据资料服从正态分布。备择假设 H1:数据资料不服从正态分布。当样本量 n≤2000 时,应选用 shapiro-wilk 检验法,检验统计量为W 值越接近于 1,P 值越大,表明资料越服从正态分布,反之 W 越偏离 1,P 值越小,表明资料越不服从正态分布。当 n>2000 时,应用 Kolmogorov-smirnov 检验法,检验统计量为D 值越大,P 值越小,表明资料越不服从正态分布,反之,D 值越小,P 值越大,表明资料越服从正态分布。在 proc univariate 语句中加上 normal 选项可以进行正态性检验。【例 1】检验数据集 sasuser.gpa 中变量 gpa 是否服从正态分布?输出结果中正态检验部分为:分析:检验的零假设为 Ho:gpa 变量服从正态分布,其中 shapiro-wilk 检验的统计量为 w=0.966294,检验的 p 值小于 0.0001,当然小于给定的显著性水平 α,故应拒绝零假设,即有 95%把握认为 gpa 非正态。说明:使用 SAS 软件中的“分析家”,打开数据集后,利用菜单“统计”→“描述性统计”→“分布”,除了可以检验变量是否服从正态分布外,还可以检验对数正态、指数和韦布尔分布。4.1.2 单样本均值的 T 检验(univariate 过程)设总体 X~N(μ,σ2),μ、σ2未知,给定检验水平 α,对常数 μ0要检验H0: μ=μ0↔H1: μ≠μ0设 X1,X2,…Xn 为 X 的简单随机样本,在 H0 成立时有t=¯X−μ0S/√n ~t (n−1)其中 S 为变量的标准差,n 为样本量。检验的拒绝域为:W ={|t|>tα(n−1)}补充 P 值检验法:分位数 t1-α/2(n-1)满足 Pr{|t|> t1-α/2(n-1)}=α设由已经得到的样本具体计算得到的 t 值为 t0,若|t0|> t1-α/2(n-1),则拒绝 H0,否则接受 H0。对大量重复试验而言,t 是随机变量,且服从 t 分...