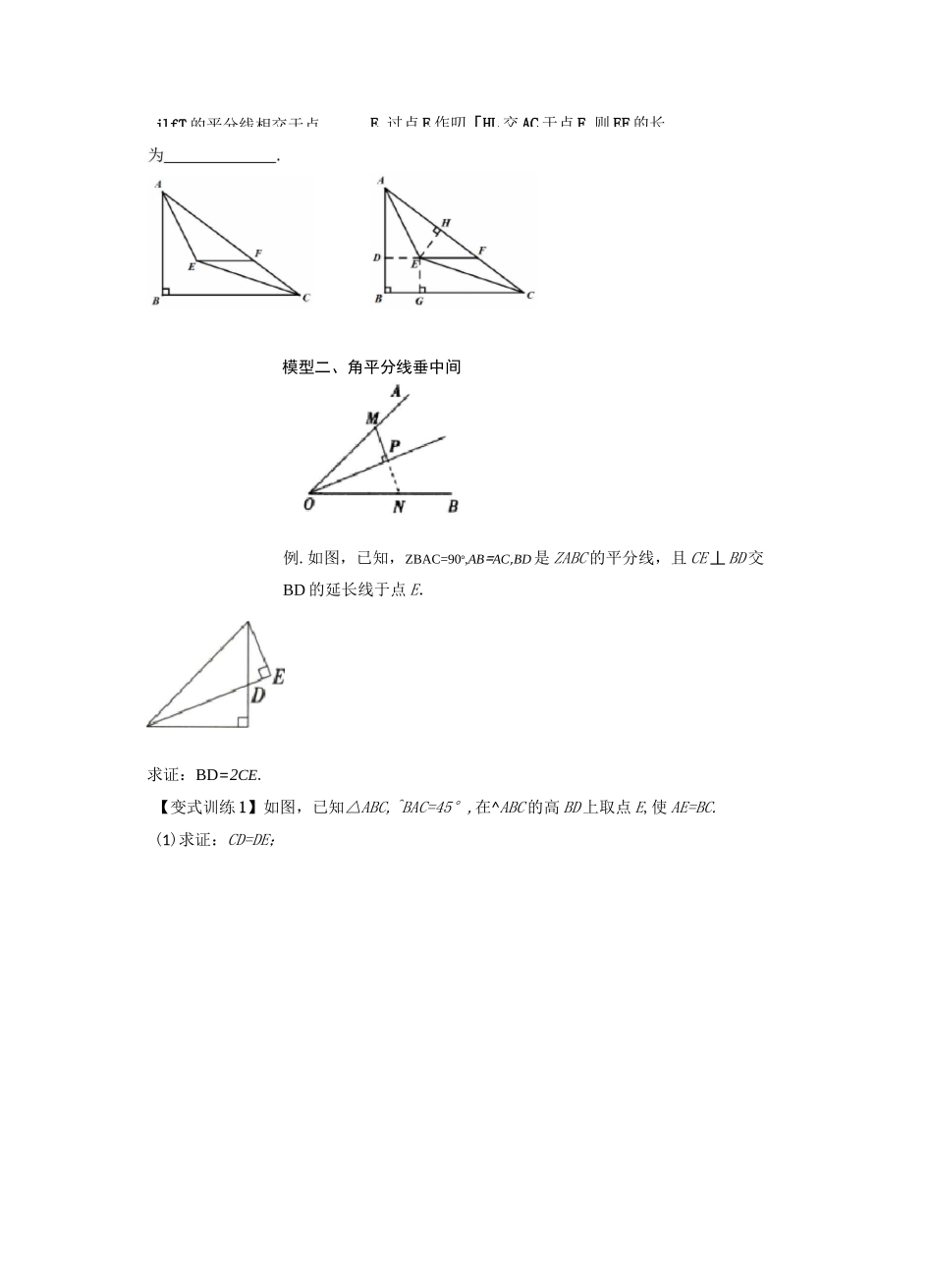
专题 01 角平分线的五种模型模型一、角平分线垂两边【变式训练 1】如图所示,在四边形 ABCD 中,DC//AB,/DAB=90°,AC 丄 BC,AC=BC,BF/ABC 的平分线交 AD,AC 于点 E、F,则——的值是EF【变式训练 2】如图,BD 平分 ABC 的外角△ABP,DA=DC,DE^BP 于点 E,若 AB=5,BC=3,求 BE的长.例 1.如图,,W 是△ABC 的角平分线,且 AB:AC=3:2,则△ABD 与^ACD 的面积之比为A.3B.6:C.2:D.不能确定例 2.如图,△A0P=^B0P=15°,PC//OA,PD^OA,若 PC=4,则 PD 的长为ACBPE【变式训练 3】如图,在『‘my(-中,=,山=厲一 w,丄打jlfT 的平分线相交于点E,过点 E 作叨[HL 交 AC 于点 F,则 EF 的长模型二、角平分线垂中间例.如图,已知,ZBAC=90o,AB=AC,BD 是 ZABC 的平分线,且 CE 丄 BD 交BD 的延长线于点 E.求证:BD=2CE.【变式训练 1】如图,已知△ABC,^BAC=45°,在^ABC 的高 BD 上取点 E,使 AE=BC.(1)求证:CD=DE;【变式训练 3】如图,在 AABC 中,CD 是 ZACB 的平分线,AD 丄 CD 于点 D,DE//BC 交 AB 于点 E,求证:EA=EB.模型三、角平分线+平行线构造等腰三角形例•如图所示,在 AMC 中,BC=6,E、F 分别是 AB、AC 的中点,动点 P 在射线 EF 上,BP 交 CE 于 D,/CBP 的平分线交 CE 于 Q,当 CQ=1CE 时,EP+BP=变式训练 1】如图,于点 C,"f'=丨,ZAOB30°求 OC 的长?变式训练2】,ZC=90°,AD 平分 ZCAB,BE 平分 ZABC,AD、BE 相交于点 F,且,贝 yAC=模型四、利用角平分线作对称(2)如图 2,若 AB=5,请直接写出 AC 的长.模型五、内外模型分线相交于点 D,则 ZD 的度数为()B.17.5°C.20°D.22.5°【变式训练】如图,匚的外角 d 的平分线 CP 与内角一 W 的平分线 BP 交于点 P,若:ijJ,则=.1.如图,BD 是•:ABC 的外角△ABP 的角平分线,DA=DC,DE^BP 于点 E,若 AB=5,BC=3,则 BE 的长为()PEBCA.2B.1.5C.1D.02.如图,AD 是 AABC 中 ZBAC 的平分线,DE 丄 AB 交 AB 于点 E,DF 丄 AC 交 AC 于点 F,3若 S=7,DE=-,AB=5,则 AC 的长为()△ABC2A.15课后训练D4MB”C例.如图,在厶 ABC 中,AB=AC,ZA=30°,E 为 BC 延长线上一点,ZABC 与 ZACE 的平4.如图,已知在四边形 ABCD 中,13A.B.4C.5D.633 如图,在 Rt^ABC 中,甌=90°,△BAC 的平分线交 BC 于点 D,CD=2,BD=3,Q 为 AB上一动点,...