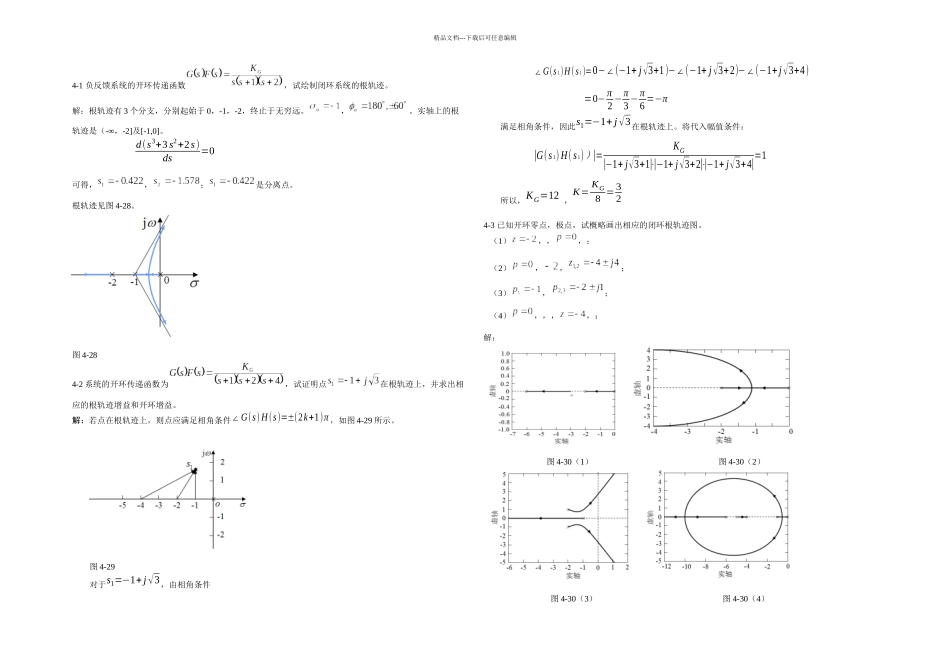
精品文档---下载后可任意编辑4-1 负反馈系统的开环传递函数,试绘制闭环系统的根轨迹。解:根轨迹有 3 个分支,分别起始于 0,-1,-2,终止于无穷远。,。实轴上的根轨迹是(-∞,-2]及[-1,0]。d(s3+3 s2+2s)ds=0可得,,;是分离点。根轨迹见图 4-28。图 4-284-2 系统的开环传递函数为,试证明点在根轨迹上,并求出相应的根轨迹增益和开环增益。解:若点在根轨迹上,则点应满足相角条件∠G(s)H(s)=±(2k+1)π ,如图 4-29 所示。图 4-29对于s1=−1+ j√3,由相角条件∠G(s 1)H(s 1)=0−∠(−1+ j√3+1)−∠(−1+ j√3+2)−∠(−1+j√3+4)=0−π2 −π3 −π6 =−π满足相角条件,因此s1=−1+ j√3在根轨迹上。将代入幅值条件:|G(s 1)H(s 1))|=KG|−1+ j√3+1|⋅|−1+ j√3+2|⋅|−1+ j√3+4|=1所以,KG=12 ,K= KG8 = 324-3 已知开环零点,极点,试概略画出相应的闭环根轨迹图。 (1),,,; (2),,; (3),; (4),,,,;解:图 4-30(1) 图 4-30(2)图 4-30(3) 图 4-30(4)精品文档---下载后可任意编辑4-4 设单位反馈控制系统开环传递函数为 试概略绘出其闭环根轨迹图(要求确定根轨迹的分离点,起始角和与虚轴的交点)。解:系统有五个开环极点:p1=0, p2=−1, p3=−3.5 , p4=−3+ j 2, p5=−3−j 21.实轴上的根轨迹:[−∞,−3.5] ,[−1,0]2.渐近线: 3.分离点: 1d + 1d+1+1d+3.5+1d+3−j 2+1d+3+ j2=0d1=−0.45,d2−2.4 (舍去) ,d3、4=−3.25± j1.904.与虚轴交点:闭环特征方程为D(s)=s(s+1)(s+3.5)(s+3+ j2)(s+3−j2)+K¿=0把s= jω 代入上方程,整理,令实虚部分别为零得:{Re(jω)=K¿+10.5ω4−79.5ω2=0¿¿¿¿可得,{ω=0¿¿¿¿ ,{ω=±1.02¿¿¿¿,{ω=±6.52¿¿¿¿(舍去) 5.根轨迹的起始角为:θp4=180∘−75..96∘−90∘−135∘−146..3∘=92..74∘由对称性得,另一起始角为92.74∘,根轨迹如图习题 4-31 所示。图 4-314-5 已知单位负反馈控制系统的开环传递函数G (s )=30 (s+b )s (s+10 )试作出以 b 为参量的根轨迹图。解:作等效开环传递函数 G(s)=30bs(s+40)1.实轴上的根轨迹:[−40,−0]2.分离点: 1d +1d+40=0解得:d=−20根轨迹如图 4-32 所示。 图 4-324-6 单位反馈系统的开环传递函数为精品文档---下载后可任意编辑G( s)=K G(s2−2s+5)(s+2)( s−0.5) 试绘制系统根轨迹,确定使系统稳定的值范围...