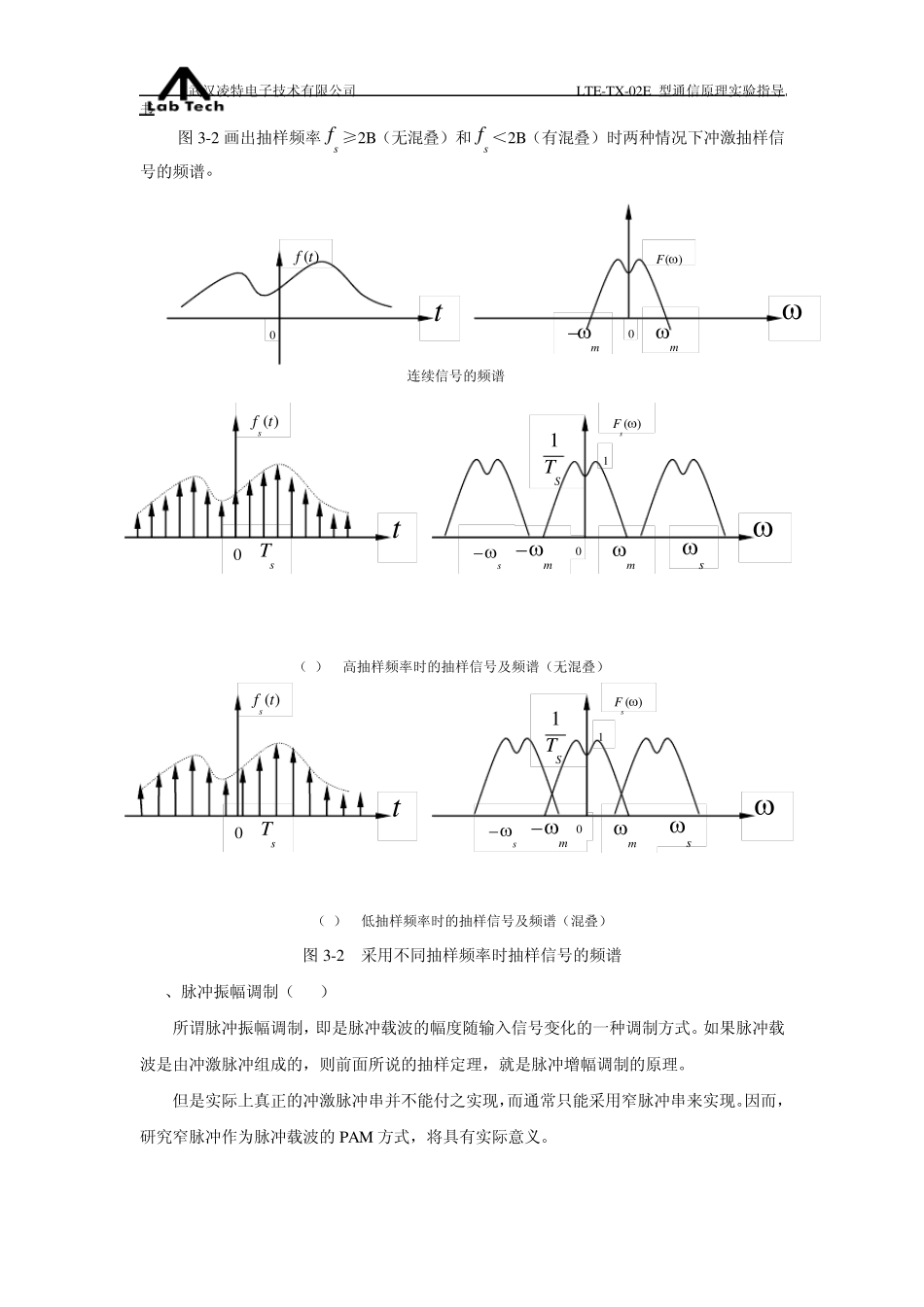
武汉凌特电子技术有限公司 LTE-TX-02E 型通信原理实验指导书 实验三 抽样定理和 PAM 调制解调实验 一、实验目的 1、 通过脉冲幅度调制实验,使学生能加深理解脉冲幅度调制的原理。 2、 通过对电路组成、波形和所测数据的分析,加深理解这种调制方式的优缺点。 二、实验内容 1、 观察模拟输入正弦波信号、抽样时钟的波形和脉冲幅度调制信号,并注意观察它们之间的相互关系及特点。 2、 改变模拟输入信号或抽样时钟的频率,多次观察波形。 三、实验器材 1、 信号源模块 一块 2、 ①号模块 一块 3、 20M双踪示波器 一台 4、 连接线 若干 四、实验原理 (一)基本原理 1、抽样定理 抽样定理表明:一个频带限制在(0,Hf)内的时间连续信号 ( )mt ,如果以 T≤Hf21秒的间隔对它进行等间隔抽样,则 ( )mt 将被所得到的抽样值完全确定。 假定将信号 ( )mt 和周期为 T 的冲激函数)t(T相乘,如图 3-1 所示。乘积便是均匀间隔为 T 秒的冲激序列,这些冲激序列的强度等于相应瞬时上 ( )mt 的值,它表示对函数 ( )mt 的抽样。若用( )m ts表示此抽样函数,则有: ( )( )( )sTm tm tt 武汉凌特电子技术有限公司 LTE-TX-02E 型通信原理实验指导书 图3-1 抽样与恢复 假设( )m t 、( )T t和( )sm t 的频谱分别为( )M 、( )T 和( )sM 。按照频率卷积定理,( )m t( )T t的傅立叶变换是( )M 和( )T 的卷积: 1( )( )( )2sTMM 因为 2()TTsnnT Ts2 所以 1( )( )()sTsnMMnT 由卷积关系,上式可写成 1( )()ssnMMnT 该式表明,已抽样信号( )m ts的频谱( )Ms 是无穷多个间隔为ω s的( )M 相迭加而成。这就意味着( )Ms 中包含( )M 的全部信息。 需要注意,若抽样间隔 T 变得大于Hf21,则( )M 和( )T 的卷积在相邻的周期内存在重叠(亦称混叠),因此不能由( )Ms 恢复( )M 。可见,HfT21是抽样的最大间隔,它被称为奈奎斯特间隔。 上面讨论了低通型连续信号的抽样。如果连续信号的频带不是限于 0 与Hf之间,而是限制在Lf (信号的最低频率)与Hf(信号的最高频率)之间(带通型连续信号),那么,其抽样频率sf 并不要求达到Hf2,而是达到 ...