小升初数学专题二阴影面积常用方法

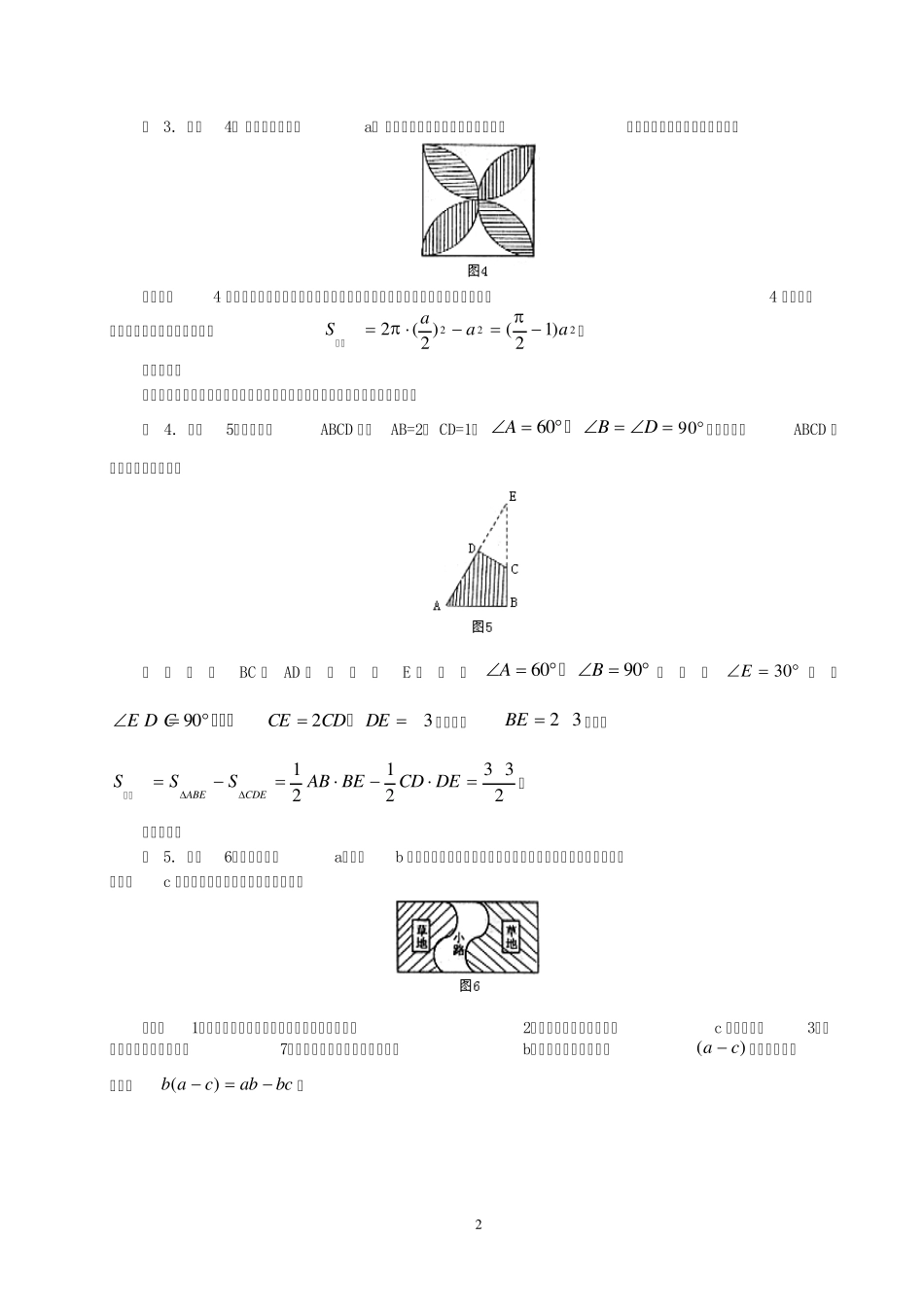
1 2015 小升初数学 专题二《阴影面积常用方法》 计算平面图形的面积问题是常见题型，求平面阴影部分的面积是这类问题的难点。不规则阴影面积常常由三角形、四边形、弓形、扇形和圆、圆弧等基本图形组合而成的，在解此类问题时，要注意观察和分析图形，会分解和组合图形。现介绍几种常用的方法。 一、转化法 此法就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积相等的规则图形，再利用规则图形的面积公式，计算出所求的不规则图形的面积。 例 1. 如图1， 点 C、 D 是以AB 为直径的半圆O 上的三等分点，AB=12， 则图中由弦AC、 AD 和 CD⌒围成的阴影部分图形的面积为_________。 分析：连结CD、 OC、 OD，如图2。易证AB//CD，则ACDOCD和的面积相等，所以图中阴影部分的面积就等于扇形OCD 的面积。易得COD6 0，故SSOCD阴影扇形6 063 6 062 。 二、和差法 有一些图形结构复杂，通过观察，分析出不规则图形的面积是由哪些规则图形组合而成的，再利用这些规则图形的面积的和或差来求，从而达到化繁为简的目的。 例 2. 如图3 是一个商标的设计图案，AB=2BC=8， ADE⌒为 14 圆，求阴影部分面积。 分 析：经观察图3 可 以分解出以下规则图形：矩形ABCD、扇形ADE、 Rt EBC。所以，SSSSADEABCDRt EBC阴影扇形矩形9 043 6 0481241 2482。 三、重叠法 就是把所求阴影部分的面积问题转化为可求面积的规则图形的重叠部分的方法。这类题阴影一般是由几个图形叠加而成。要准确认清其结构，理顺图形间的大小关系。 2 例 3. 如图4， 正方形的边长为a， 以各边为直径在正方形内作半圆，求所围成阴影部分图形的面积。 解：因为4 个半圆覆盖了正方形，而且阴影部分重叠了两次，所以阴影部分的面积等于4 个半圆的面积和与正方形面积的差。故Saaa阴影2221222( )()。 四、补形法 将不规则图形补成特殊图形，利用特殊图形的面积求出原不规则图形的面积。 例 4. 如图5，在四边形ABCD 中，AB=2， CD=1，  ABD60 ，9 0  ，求四边形ABCD 所在阴影部分的面积。 解：延长BC 、AD ，交于点E ，因为AB6090，，所以E3 0，又E D CCECDDE9023，所以，，易求得BE  23 ，所以 SSSAB BECD DEABECDE阴影1212332。 五、拼接法 例 5. ...