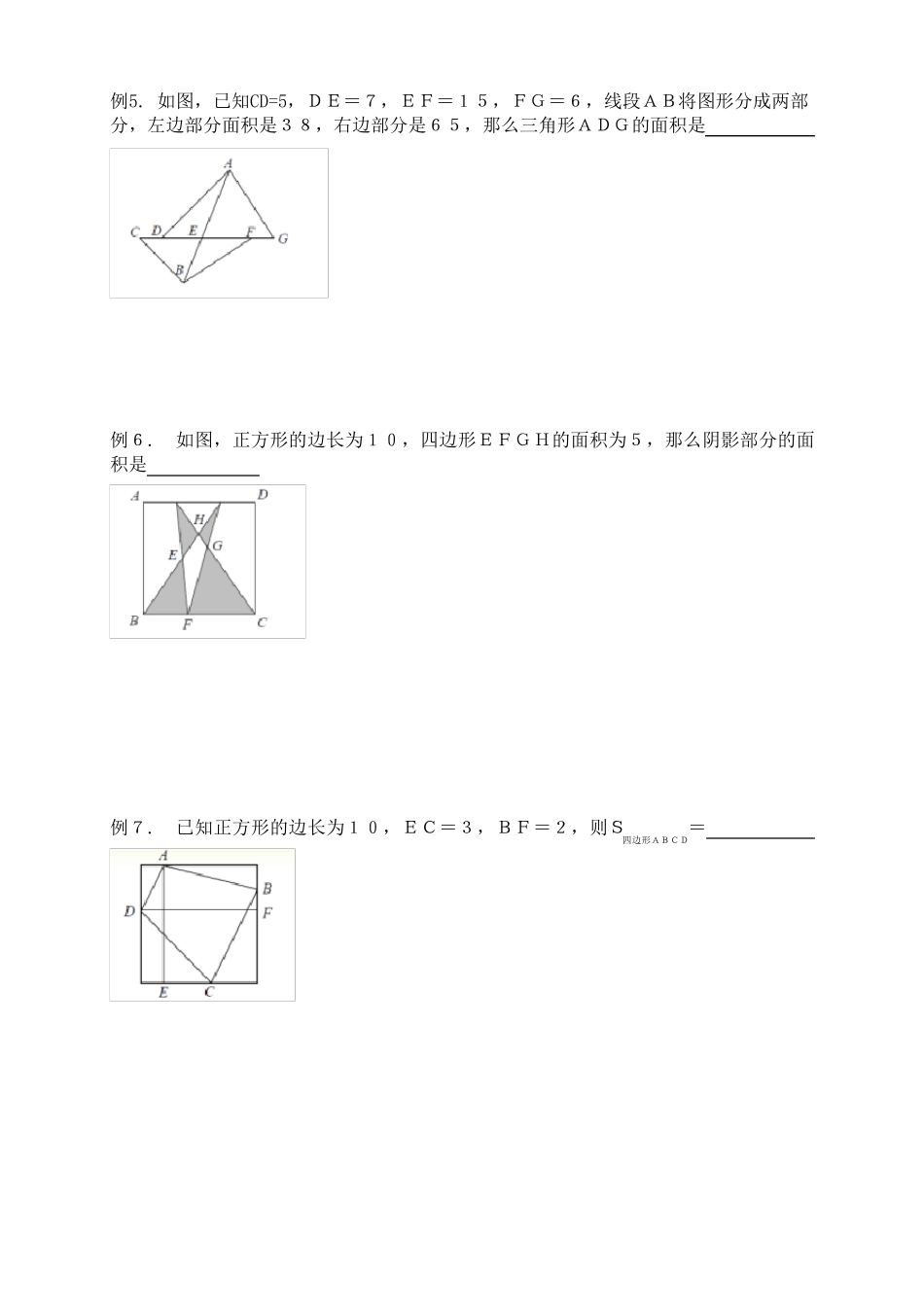
等积变换与共角定理 我们的目标:掌握三角形等积变换与共角定理的基本模型;学会构造出模型进行解题 三角形等积变换模型 (1)等底等高的两个三角形面积相等; (2)两个三角形高相等,面积比等于底之比;如左图1 2 : :S S a b (3)两个三角形底相等,面积比等于高之比; 在一组平行线之间的等积变形,如右图; S△ACD=S△BCD; 共角定理 两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如下两图 例1. 如图三角形ABC的面积为1,其中AE=3AB,BD=2BC,三角形BDE的面积是多少? 例2. 如图,三角形ABC的面积是24,D、E分别是BC、AC和AD的中点,求三角形DEF的面积。 例3. 如图,在角MON的两边上分别有A、C、E及B、D、F六个点,并且△ OAB、 △ABC、 △BCD、 △CDE 、△DEF 的面积都等于1,则△DCF的面积等于 例4. E、M分别为直角梯形ABCD两边的点,且DQ、CP、ME彼此平行,若AD=5,BC=7,AE=5,EB=3.求阴影部分的面积 例5. 如图,已知CD=5,DE=7,EF=15,FG=6,线段AB将图形分成两部分,左边部分面积是38,右边部分是65,那么三角形ADG的面积是 例6. 如图,正方形的边长为10,四边形EFGH的面积为5,那么阴影部分的面积是 例7. 已知正方形的边长为10,EC=3,BF=2,则S四边形ABCD= 例8.如图,平行四边形ABCD,BE=AB,CF=2BC,DG=3DC,HA=4AD,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比。 例9. 已知△DEF的面积为7平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积 等积变换与共角定理习题 1. 如图,在长方形ABCD中,Y是BD的中点,Z是DY的中点,如果AB=24厘米,BC=8厘米,求三角形ZCY的面积 2. 如图,点D、E、F在线段CG上,已知CD=2厘米,DE=8厘米,EF=20厘米,FG=4厘米,AB将整个图形分成上下两部分,下边部分面积是67平方厘米,上边部分是166平方厘米,则三角形ADG的面积是多少平方厘米? 3. 如图,阴影部分四边形的外界图形是边长为12厘米的正方形,则阴影部分四边形的面积是多少平方厘米? 4. 如图,四边形EFGH的面积是66平方米,EA=AB,CB=BF,DC=CG,HD=DA,求四边形ABCD的面积。 5. 如图,在△ABC中,延长AB至D,是BD=AB,延长BC至E,使CE= 21 BC,F是AC的中点,若△ABC的面积是2,则△DEF的面积是多少? 6. 如图,S△ABC=1,BC=5BD,AC=4EC,DG=GS=SE,AF=FG,求S△FGS 7. 如图,正方形ABCD的边长为6,AE=1.5,CF=2,长方形EFG和的面积为 8. 如图,已知三角形ABC面积为1,延长AB至D,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。