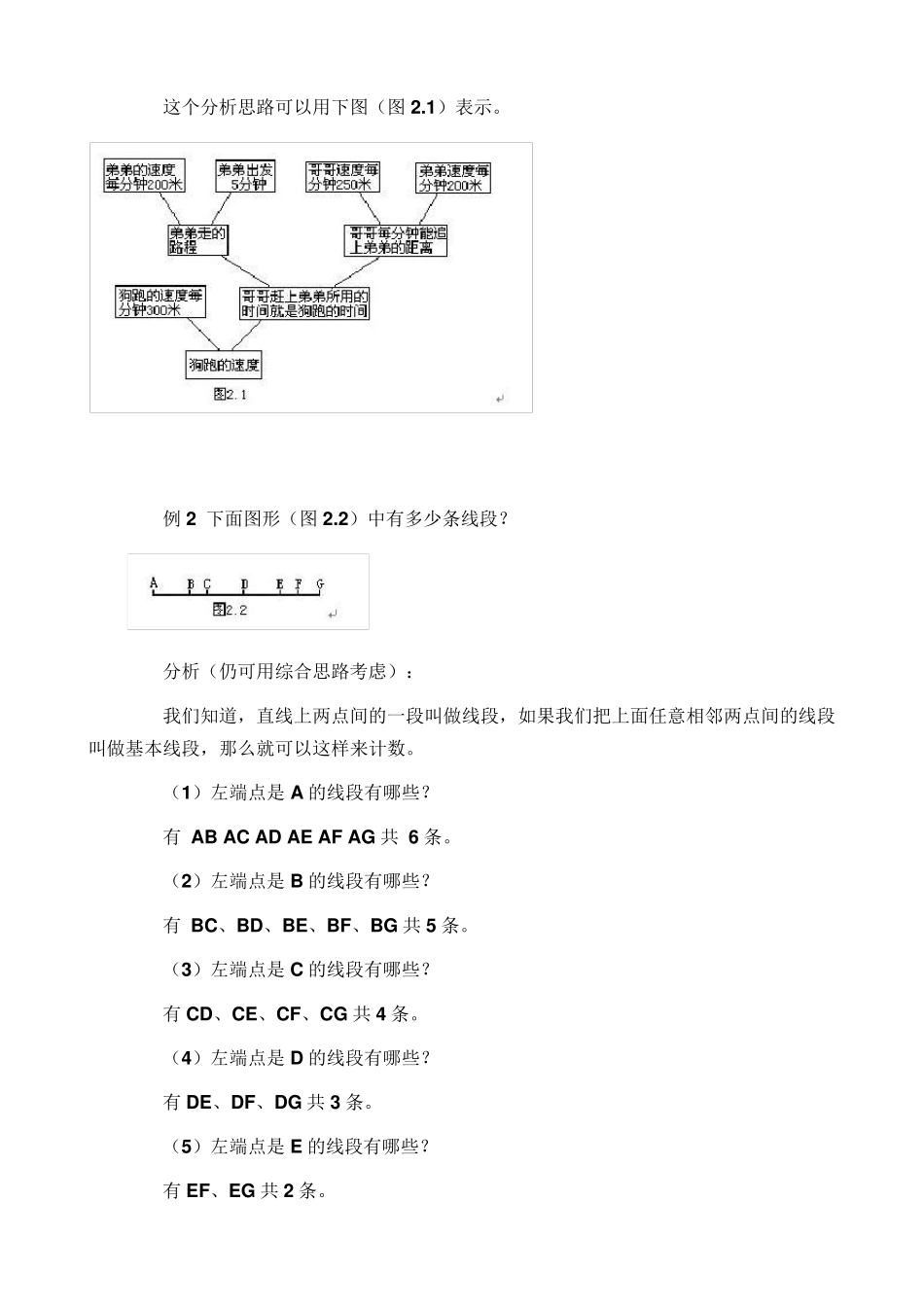
小 学 数 学 常 用 的 十 一种解题思路 一、直接思路 (本文选自:小学数学解题方法、思路、技巧汇编 点击) “直接思路”是解题中的常规思路。它一般是通过分析、综合、归纳等方法,直接找到解题的途径。 【顺向综合思路】从已知条件出发,根据数量关系先选择两个已知数量,提出可以解决的问题;然后把所求出的数量作为新的已知条件,与其他的已知条件搭配,再提出可以解决的问题;这样逐步推导,直到求出所要求的解为止。这就是顺向综合思路,运用这种思路解题的方法叫“综合法”。 例 1 兄弟俩骑车出外郊游,弟弟先出发,速度为每分钟 2 0 0 米,弟弟出发 5 分钟后,哥哥带一条狗出发,以每分钟 2 5 0 米的速度追赶弟弟,而狗以每分钟 3 0 0 米的速度向弟弟追去,追上弟弟后,立即返回,见到哥哥后又立即向弟弟追去,直到哥哥追上弟弟,这时狗跑了多少千米? 分析(按顺向综合思路探索): (1 )根据弟弟速度为每分钟 2 0 0 米,出发 5 分钟的条件,可以求什么? 可以求出弟弟走了多少米,也就是哥哥追赶弟弟的距离。 (2 )根据弟弟速度为每分钟 2 0 0 米,哥哥速度为每分钟 2 5 0 米,可以求什么? 可以求出哥哥每分钟能追上弟弟多少米。 (3 )通过计算后可以知道哥哥追赶弟弟的距离为 1 0 0 0 米,每分钟可追上的距离为5 0 米,根据这两个条件,可以求什么? 可以求出哥哥赶上弟弟所需的时间。 (4 )狗在哥哥与弟弟之间来回不断奔跑,看起来很复 杂 ,仔 细 想 一想 ,狗跑的时间与谁 用的时间是一样的? 狗跑的时间与哥哥追上弟弟所用的时间是相 同 的。 (5 )已知狗以每分钟 3 0 0 米的速度,在哥哥与弟弟之间来回奔跑,直到哥哥追上弟弟为止,和 哥哥追上弟弟所需的时间,可以求什么? 可以求出这时狗总 共 跑了多少距离? 这个分析思路可以用下图(图2.1)表示。 例2 下面图形(图2.2)中有多少条线段? 分析(仍可用综合思路考虑): 我们知道,直线上两点间的一段叫做线段,如果我们把上面任意相邻两点间的线段叫做基本线段,那么就可以这样来计数。 (1)左端点是A 的线段有哪些? 有 AB AC AD AE AF AG 共 6 条。 (2)左端点是B 的线段有哪些? 有 BC、BD、BE、BF、BG 共5 条。 (3)左端点是C 的线段有哪些? 有CD、CE、CF、CG 共4 条。 (4)左端点是D 的线段有哪些? 有DE、DF、DG 共3 条。 (5)左端...