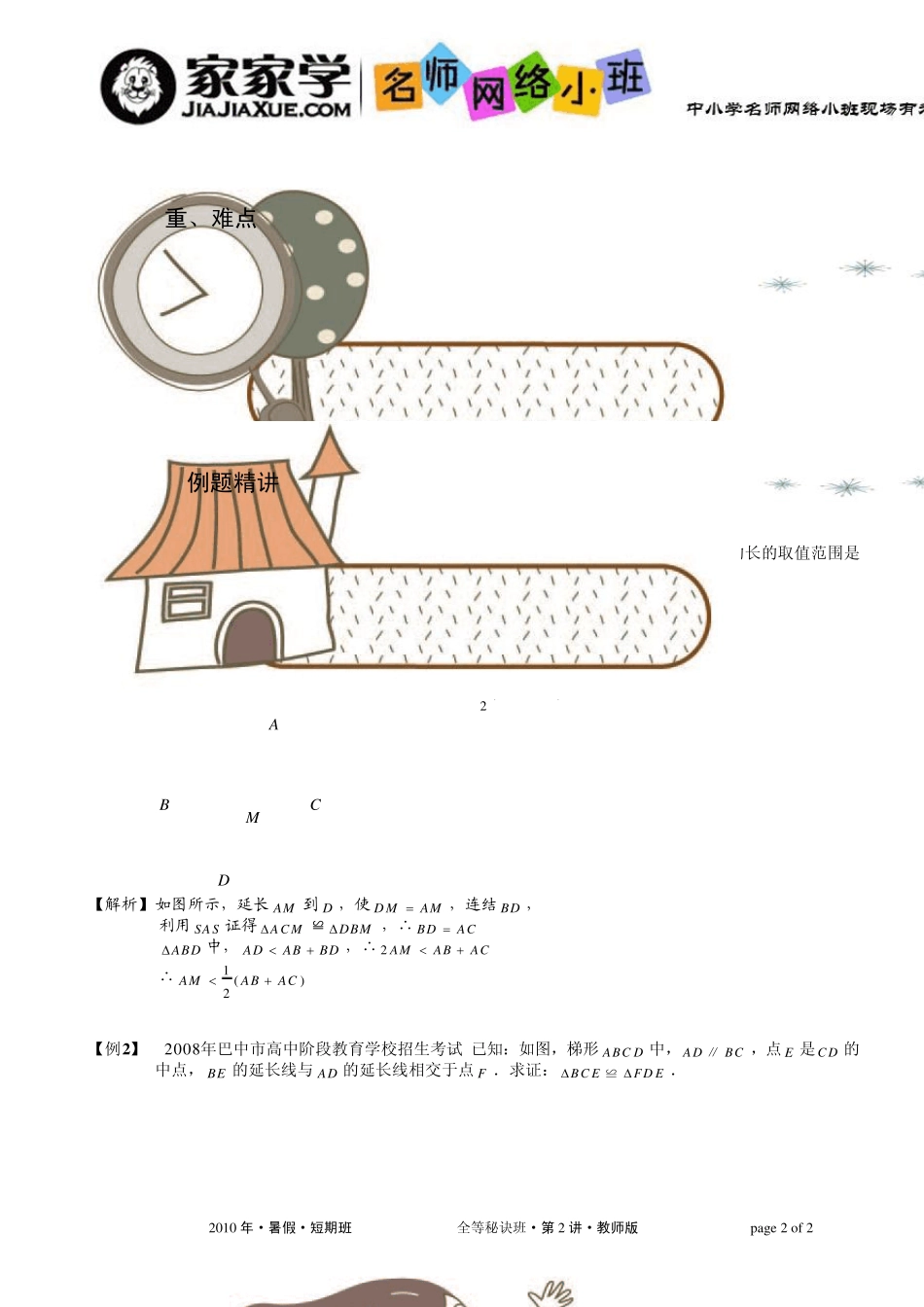
2010 年·暑假·短期班 全等秘诀班·第2 讲·教师版 p ag e 1 o f 1 板块 考试要求 A 级要求 B 级要求 C 级要求 全等三角形的性质及判定 会识别全等三角形 掌握全等三角形的概念、判定和性质,会用全等三角形的性质和判定解决简单问题 会运用全等三角形的性质和判定解决有关问题 三角形中线的定义:三角形顶点和对边中点的连线 三角形中线的相关定理: 直角三角形斜边的中线等于斜边的一半 等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合) 三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线. 三角形中位线定理:三角形的中位线平行于第三边并且等于它的一半. 中位线判定定理:经过三角形一边中点且平行于另一边的直线必平分第三边. 中线中位线相关问题(涉及中点的问题) 见到中线(中点),我们可以联想的内容无非是倍长中线以及中位线定理(以后还要学习中线长公式),尤其是在涉及线段的等量关系时,倍长中线的应用更是较为常见. 知识点睛 中考要求 第二讲 全等三角形与 中点问题 2010 年·暑假·短期班 全等秘诀班·第2 讲·教师版 p ag e 2 o f 2 版块一 倍长中线 【例1 】 (2002年通化市中考题)在△ ABC 中,9,5ACAB,则 BC 边上的中线 AD 的长的取值范围是什么? 【解析】 中线倍长,72 AD 【点评】此题很好的运用中线倍长的方法,若运用其他的方法将会更加麻烦 【补充】已知:ABC中, AM 是中线.求证:1 ()2AMABAC. AMDCB 【解析】 如图所示,延长AM 到D ,使D MAM,连结BD , 利用SA S证得AC M≌DBM,∴ BDAC ABD中,ADABBD,∴ 2 AMABAC ∴1 ()2AMABAC 【例2 】 (2008年巴中市高中阶段教育学校招生考试)已知:如图,梯形 ABC D 中,ADBC∥,点 E 是C D 的中点, BE 的延长线与 AD 的延长线相交于点 F .求证:BC EFD E≌. 重点:主要掌握中线的处理方法,遇见中线考虑中线倍长法 难点:全等三角形的综合运用 重、难点 例题精讲 2010 年·暑假·短期班 全等秘诀班·第 2 讲·教师版 p ag e 3 o f 3 DFECBA 【解析】 点E 是D C 中点 ∴ D EC E 又 ADBC∥, F 在 AD 延长线上 ∴D FEC BE ,FD EBC E 在BC E与FD E中 EBCEFDEC BED FCEDE ∴()BCEFD...