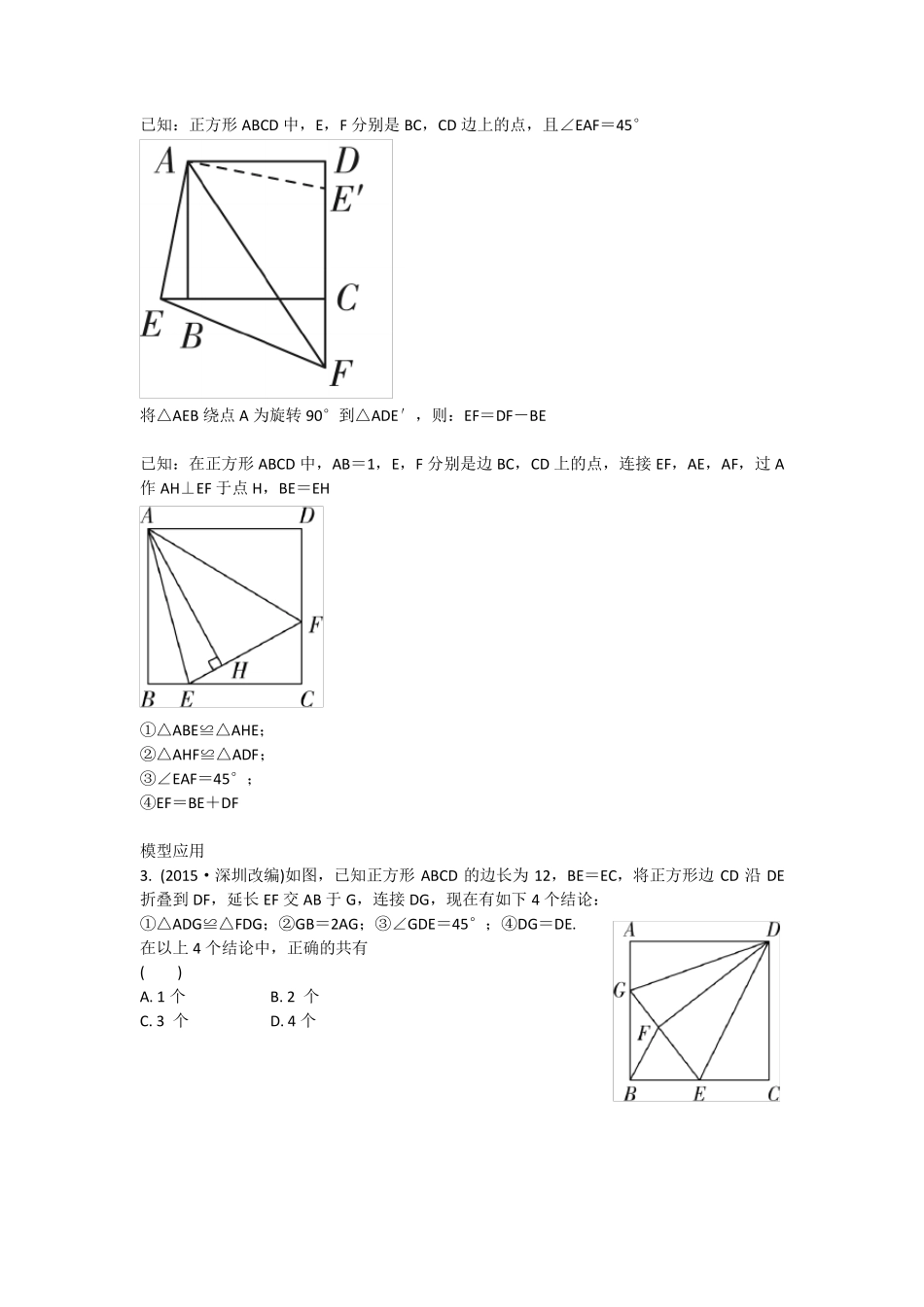
全等三角形的五种模型 手拉手模型 已知:△ABE 和△ACD 为两个的等腰三角形,∠BAE=∠CAD=∠α,连接EC,BD 交于点O ①△ABD ≌△AEC; ②∠α+∠BOC=180°; ③OA 平分∠BOC 已知:△ABD 和△ACE 均为等腰直角三角形,连接CD,BE 交于点O ①△ACD ≌△ABE; ②∠BOC=90°; ③OA 平分∠BOC 已知:直线 AB 的同一侧作△ABD 和△BCE 都为等边三角形,连接AE,CD,二者交点为H ①△ABE≌△DBC;②AE=DC;③∠DHA=60°; ④△AGB≌△DFB;⑤△EGB≌△CFB;⑥连接GF,GF∥AC;⑦连接HB,HB 平分∠AHC 模型应用 1. (2010·深圳改编)如图,△AOB 和△COD 均为等腰直角三角形,∠AOB=∠COD=90°,D在 AB 上. (1)求证:△AOC≌△BOD; (2)判断△CAD 是什么形状的三角形,说明理由. 2. 如图,△ABC 与△ADE 都是等腰直角三角形,连接 CD,BE,CD,BE 相交于点 O,判断CD 与 BE 的位置关系,并说明理由. 半角模型 已知:正方形ABCD 中,E,F 分别是 BC,CD 边上的点,且∠EAF=45 将△ADF 绕点 A 旋转 90°到△ABG,则: ①EF=DF+BE; ②△CEF 的周长为正方形ABCD 周长的一半 已知:正方形ABCD 中,E,F 分别是BC,CD 边上的点,且∠EAF=45° 将△AEB 绕点A 为旋转 90°到△ADE′,则:EF=DF-BE 已知:在正方形ABCD 中,AB=1,E,F 分别是边BC,CD 上的点,连接 EF,AE,AF,过 A作 AH⊥EF 于点H,BE=EH ①△ABE≌△AHE; ②△AHF≌△ADF; ③∠EAF=45°; ④EF=BE+DF 模型应用 3. (2015·深圳改编)如图,已知正方形ABCD 的边长为 12,BE=EC,将正方形边CD 沿 DE折叠到 DF,延长 EF 交 AB 于 G,连接 DG,现在有如下 4 个结论: ①△ADG≌△FDG;②GB=2AG;③∠GDE=45°;④DG=DE. 在以上4 个结论中,正确的共有 ( ) A. 1 个 B. 2 个 C. 3 个 D. 4 个 4. 如图,在正方形ABCD 中,AB=1,E,F 分别是边BC,CD 上的点,连接EF,AE,AF,过A 作AH⊥EF 于点H.若EF=BE+DF,那么下列结论:①AE 平分∠BEF;②FH=FD;③∠EAF=45°;④S△EAF=S△ABE+S△ADF;⑤△CEF 的周长为 2.其中正确结论的个数是( ) A. 2 B. 3 C. 4 D. 5 倍长中线模型 已知:在△ABC 中,AD 是BC 边中线 延长 AD 到 E,使 DE=AD,连接BE,则: ①△ADC≌△EDB; ②AD< 21 (AB+AC) 已知:在△ABC 中...