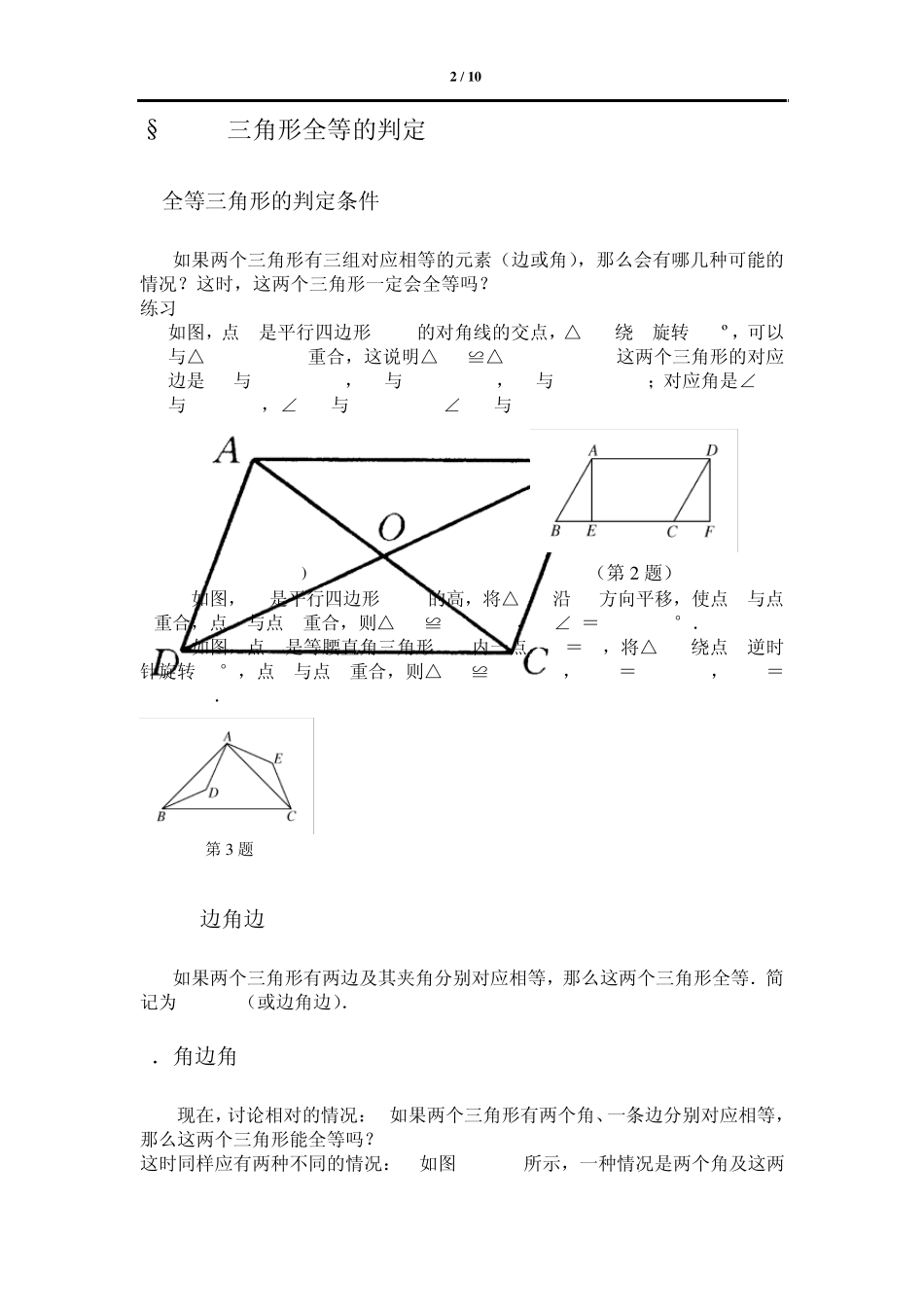
1 / 10 §19 全等三角形 §19.1 命题与定理 1.命题 可以判断它是正确的或是错误的句子叫做命题(proposition).正确的命题称为真命题,错误的命题称为假命题. 许多命题是由题设(或已知条件)、结论两部分组成的.题设是已知事项;结论是由已知事项推出的事项.这样的命题常可写成“如果„„,那么„„”的形式. 例 1 把命题“三个角都相等的三角形是等边三角形”改写成“如果„„,那么„„”的形式,并分别指出命题的题设与结论. 解 这个命题可以写成“如果一个三角形的三个角都相等,那么这个三角形是等边三角形”.这个命题的题设是“一个三角形的三个角都相等”,结论是“这个三角形是等边三角形”. 要判断一个命题是真命题, 可以用逻辑推理的方法加以论证; 而要判断一个命题是假命题,只要举出一个例子, 说明该命题不成立, 即只要举出一个符合该命题题设而不符合该命题结论的例子就可以了. 练习 1 把下列命题改写成“如果„„,那么„”的形式,并指出它的题设和结论. (1) 全等三角形的对应边相等; (2) 平行四边形的对边相等. 2 指出下列命题中的真命题和假命题. (1) 同位角相等,两直线平行; (2) 多边形的内角和等于 180°. 2 公理、定理 数学中有些命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,这样的真命题叫做公理(axioms). 我们已经知道下列命题是真命题: 一条直线截两条平行直线所得的同位角相等; 两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行; 全等三角形的对应边、对应角分别相等. 在本书中我们将这些真命题均作为公理. 从公理或其他真命题出发,用逻辑推理的方法证明它们是正确的,并且可以进一步作为判断其他命题真假的依据,这样的真命题叫做定理(theorem). 2 / 10 §19.2 三角形全等的判定 1.全等三角形的判定条件 如果两个三角形有三组对应相等的元素(边或角),那么会有哪几种可能的情况?这时,这两个三角形一定会全等吗? 练习 1. 如图,点O是平行四边形ABCD的对角线的交点,△AOB绕O旋转180º,可以与△___________重合,这说明△AOB≌△___________.这两个三角形的对应边是AO与__________,OB与__________,BA与__________;对应角是∠AOB与________,∠OBA与_________,∠BAO与___________. (第1 题) (第2 题) 2 如图,AE是平行四边形ABCD的高,将△ABE沿AD...