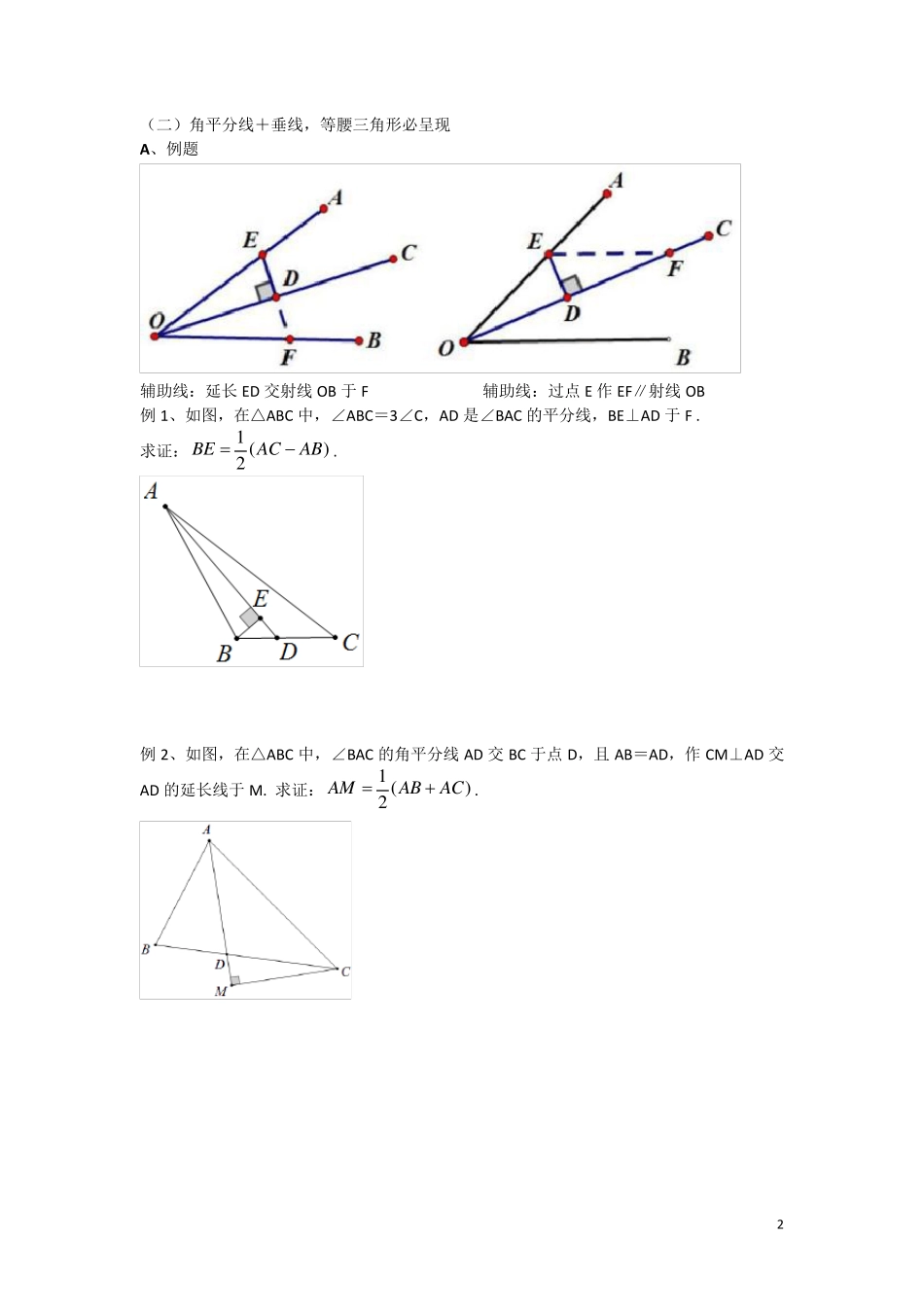
1 全等三角形相关模型总结 一、角平分线模型 (一)角平分线的性质模型 辅助线:过点G 作GE⊥射线AC A、例题 1、如图,在△ABC 中,∠C=90°,AD 平分∠CAB,BC=6cm ,BD=4cm ,那么点D 到直线AB的距离是 cm . 2、如图,已知,∠1=∠2,∠3=∠4,求证:AP 平分∠BAC. B、模型巩固 1、如图,在四边形ABCD 中,BC>AB,AD=CD,BD 平分∠ABC,求证:∠A+∠C=180°. 2 (二)角平分线+垂线,等腰三角形必呈现 A 、例题 辅助线:延长ED 交射线OB 于F 辅助线:过点E 作EF∥射线OB 例1、如图,在△ABC 中,∠ABC=3∠C,AD 是∠BAC 的平分线,BE⊥AD 于F . 求证:1 ()2BEACAB. 例2、如图,在△ABC 中,∠BAC 的角平分线AD 交BC 于点D,且 AB=AD,作CM⊥AD 交AD 的延长线于M. 求证: 1 ()2AMABAC. 3 (三)角分线,分两边,对称全等要记全 两个图形飞辅助线都是在射线ON 上取点B,使OB=OA,从而使△OAC≌△OBC . A 、例题 1、如图,在△ABC 中,∠BAC=60°,∠C=40°,AP 平分∠BAC 交 BC 于 P,BQ 平分∠ABC交 AC 于 Q ,求证:AB+BP=BQ +AQ . 2、如图,在△ABC 中,AD 是∠BAC 的外角平分线,P 是AD 上异于点A 的任意一点,试比较 PB+PC 与 AB+AC 的大小,并说明理由 . 4 B 、模型巩固 1、在△ABC 中,AB>AC,AD 是∠BAC 的平分线,P是线段AD 上任意一点(不与A 重合). 求证:AB-AC>PB-PC . 2、如图,△ABC 中,AB=AC,∠A=100°,∠B 的平分线交 AC 于 D, 求证:AD+BD=BC . 3、如图,△ABC 中,BC=AC,∠C=90°,∠A 的平分线交 BC 于 D, 求证:AC+CD=AB . 5 二、等腰直角三角形模型 (一)旋转中心为直角顶点,在斜边上任取一点的旋转全等: 操作过程: (1)将△ABD 逆时针旋转90°,得△ACM ≌ △ABD,从而推出△ADM 为等腰直角三角形. (2)辅助线作法:过点C 作MC⊥BC,使 CM=BD,连结 AM. (二)旋转中心为斜边中点,动点在两直角边上滚动的旋转全等: 操作过程:连结 AD. (1)使 BF=AE(或 AF=CE),导出△BDF ≌ △ADE. (2)使∠EDF+∠BAC=180°,导出△BDF ≌ △ADE. A 、例题 1、如图,在等腰直角△ABC 中,∠BAC=90°,点M、N在斜边BC 上滑动,且∠MAN=45°,试探究 BM、MN、CN之间的数量关系. 6 2、两个全等的含有30°,60°角的直角三角板 A...