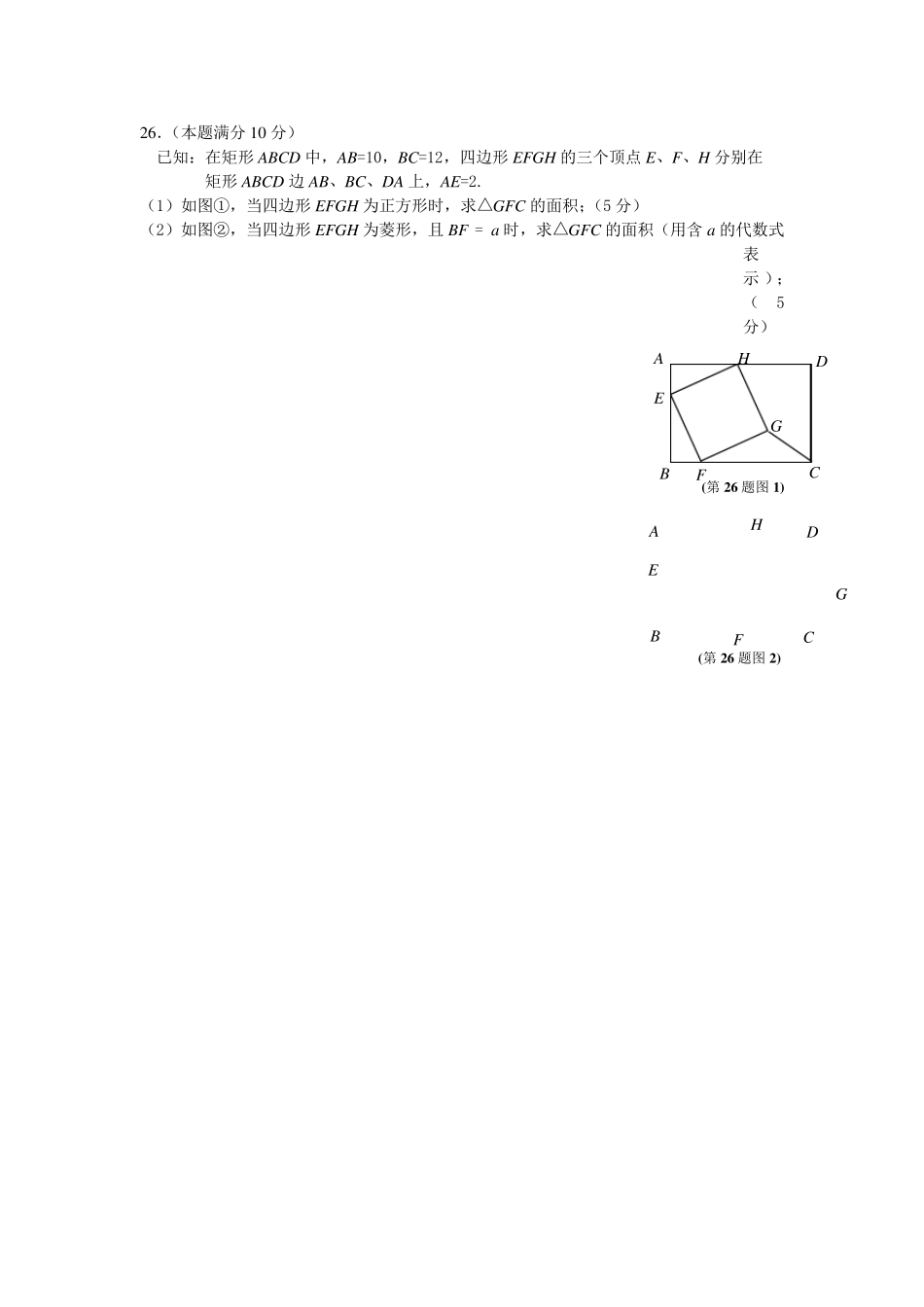
2 6 .(本题满分1 0 分) 已知:在矩形ABCD 中,AB=10,BC=12,四边形EFGH 的三个顶点E、F、H 分别在 矩形ABCD 边AB、BC、DA 上,AE=2. (1)如图①,当四边形EFGH 为正方形时,求△GFC 的面积;(5 分) (2)如图②,当四边形EFGH 为菱形,且 BF = a时,求△GFC 的面积(用含 a的代数式表示 );(5分) D C A B E (第 2 6 题图1 ) F H G D C A B E (第 2 6 题图2 ) F H G 26.解:(1)如图①,过点G 作GMBC于M. …………………………………………(1分) 在正方形 EFGH 中, 90 ,HEFEHEF. …………………………………………………………(1分) 90.90 ,.AEHBEFAEHAHEAHEBEF 又 90AB , ∴⊿AHE≌⊿BEF …………………………………………………………(1分)同理可证:⊿MFG≌⊿BEF. …………………………………………………………(1 分) ∴GM=BF=AE=2. ∴FC=BC-BF=10. …………………………………………………………(1分 ) (2 )如图② ,过点G作GMBC于M. 连 接HF. …………………………………………(1 分) //,.//,.ADBCAHFMFHEHFGEHFGFH .AHEMFG …………………………………………………(1分) 又90 ,,AGMFEHGF ∴⊿AHE≌⊿MFG. ………………………………………………………(1分) ∴GM=AE=2. ……………………………………………………………(1分) 11 (12)12.22GFCSFC GMaa …………………………………………(1分) 如图,直线 343yx 与x 轴相交于点A ,与直线3yx相交于点P . (1) 求点P 的坐标. (2) 请判断△OPA 的形状并说明理由. (3) 动点E 从原点O 出发,以每秒 1 个单位的速度沿着OPA的路线向点A 匀速运动( E 不与点O 、A 重合),过点E 分别作 EFx 轴于F ,EBy 轴于B .设运动t秒时,矩形 EBOF 与△OPA 重叠部分的面积为 S .求S 与t 之间的函数关系式. FBEPAOxy (备 用 图)PAOxy 解:(1)3433yxyx 解得:223xy ………………………1′ ∴ 点 P 的坐标为(2,23 ) ………………………1′ (2)当0y 时,4x ∴点 A 的坐标为(4,0) ………………………1′ 222234OP 22(24 ...