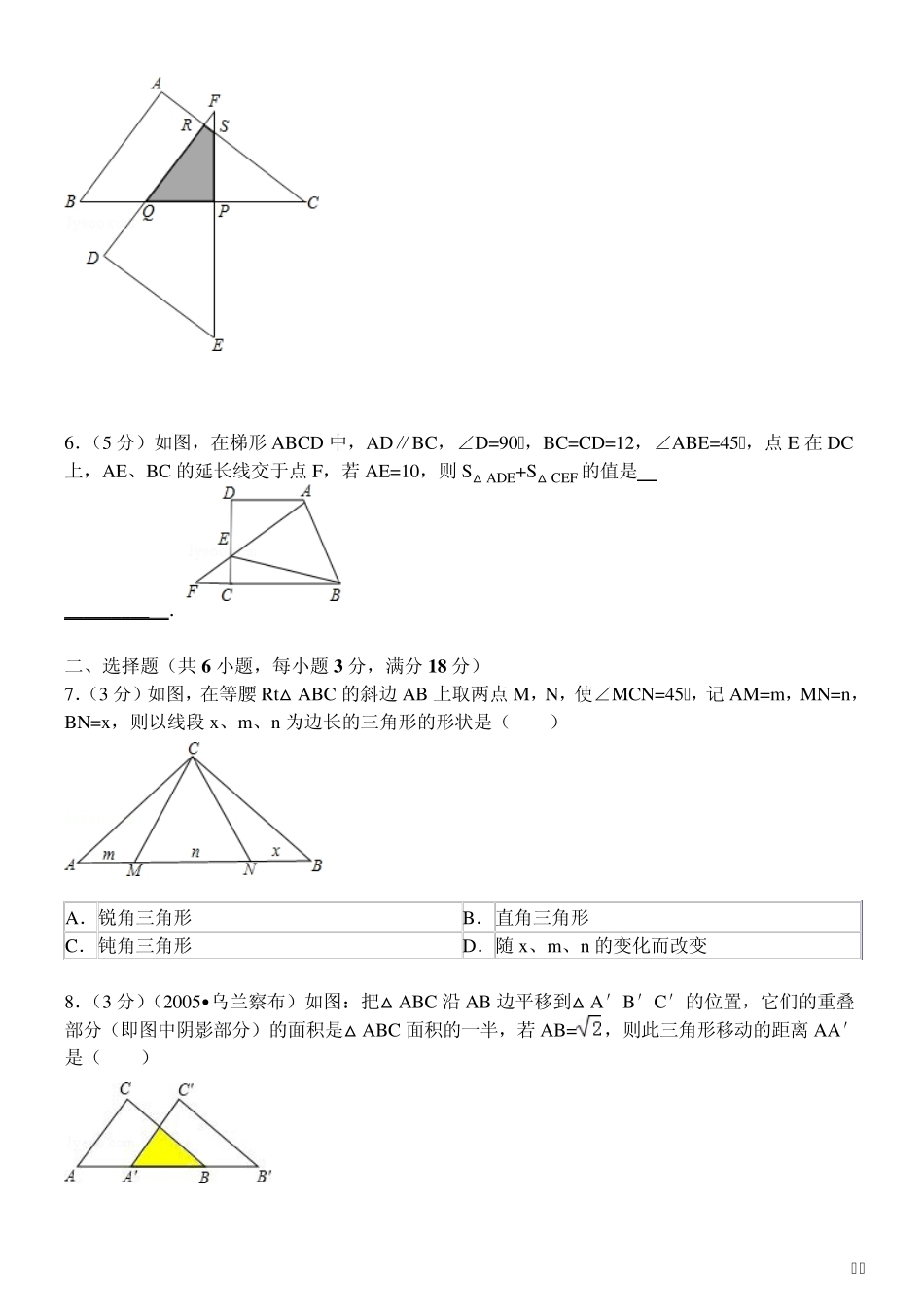
八年级数学竞赛培训图形的平移与旋转 一、填空题(共6 小题,每小题5 分,满分3 0 分) 1.(5 分)如图,P 为正方形ABCD 内一点,PA:PB:PC=1:2:3,则∠APB= _________ . 2.(5 分)(2002•河南)如图,P 是正方形ABCD 内一点,将△ABP 绕点B 顺时针方向旋转能与△CBP′重合,若 PB=3,则PP′= _________ . 3.(5 分)如图,P 是等边△ABC 内一点,PA=6,PB=8,PC=10,则∠APB= _________ . 4.(5 分)如图,四边形ABCD 中,AB∥CD,∠D=2∠B,若 AD=a,AB=b,则CD 的长是 _________ . 5.(5 分)(2002•济南)在 Rt△ABC 中,∠A=90°,AB=3cm,AC=4cm,以斜边 BC 上距离 B 点3cm 的点P 为中心,把这个三角形按逆时针方向旋转90°到 Rt△DEF,则旋转前后两个直角三角形重叠部分的面积为 _________ cm2. 2 6.(5 分)如图,在梯形ABCD 中,AD∥BC,∠D=90°,BC=CD=12,∠ABE=45°,点E 在DC上,AE、BC 的延长线交于点F,若AE=10,则S△ADE+S△CEF 的值是 _________ . 二、选择题(共6 小题,每小题3 分,满分18 分) 7.(3 分)如图,在等腰Rt△ABC 的斜边AB 上取两点M,N,使∠MCN=45°,记AM=m,MN=n,BN=x ,则以线段x 、m、n 为边长的三角形的形状是( ) A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 随x 、m、n 的变化而改变 8.(3 分)(2005•乌兰察布)如图:把△ABC 沿AB 边平移到△A′B′C′的位置,它们的重叠部分(即图中阴影部分)的面积是△ABC 面积的一半,若AB=,则此三角形移动的距离 AA′是( ) 3 A. ﹣1 B. C. 1 D. 9.(3 分)如图,已知△ABC 中,AB=AC,∠BAC=90°,直角∠EPF 的顶点 P 是 BC 中点,两边PE、PF 分别交 AB、AC 于点 E、F,给出以下四个结论: ①△PFA≌△PEB; ②∠PFE=45°; ③EF=AP; ④图中阴影部分的面积是△ABC 的面积的一半; 当∠EPF 在△ABC 内绕顶点 P 旋转时(点 E 不与 A,B 重合),上述结论中始终正确的有( ) A. 1 个 B. 2 个 C. 3 个 D. 4 个 10.(3 分)(2009•临夏州)如图,四边形 ABCD 中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD 于点 E,且四边形 ABCD 的面积为 8,则 BE=( ) A. 2 B. 3 C. D. 11.(3 分)如图,在△ABC 中,∠BAC=120°,P 是△ABC 内一点,则( ) A. PA+P...