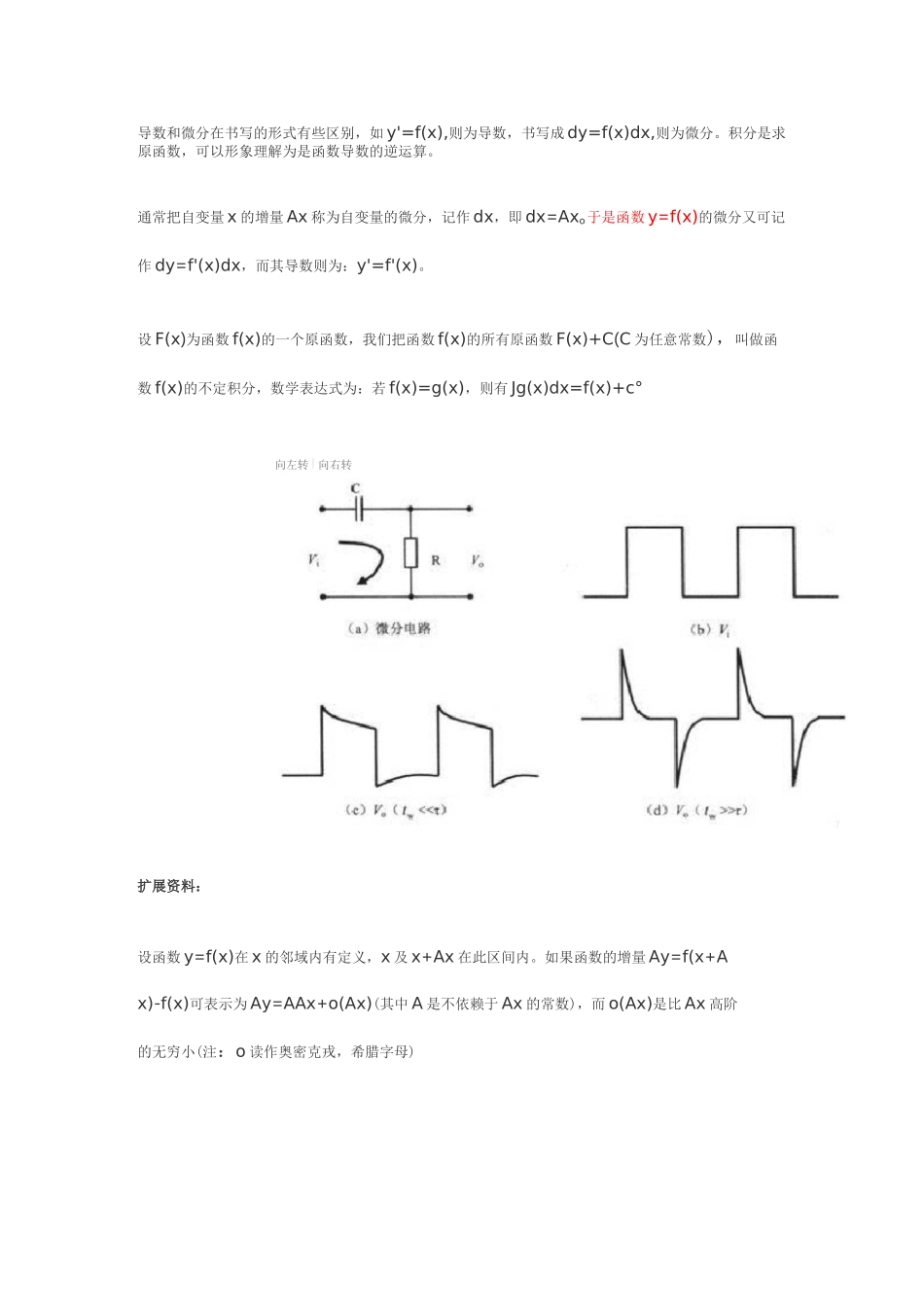
导数和微分在书写的形式有些区别,如 y'=f(x),则为导数,书写成 dy=f(x)dx,则为微分。积分是求原函数,可以形象理解为是函数导数的逆运算。通常把自变量 x 的增量 Ax 称为自变量的微分,记作 dx,即 dx=Axo于是函数 y=f(x)的微分又可记作 dy=f'(x)dx,而其导数则为:y'=f'(x)。设 F(x)为函数 f(x)的一个原函数,我们把函数 f(x)的所有原函数 F(x)+C(C 为任意常数),叫做函数 f(x)的不定积分,数学表达式为:若 f(x)=g(x),则有 Jg(x)dx=f(x)+c°向左转 I 向右转扩展资料:设函数 y=f(x)在 x 的邻域内有定义,x 及 x+Ax 在此区间内。如果函数的增量 Ay=f(x+Ax)-f(x)可表示为 Ay=AAx+o(Ax)(其中 A 是不依赖于 Ax 的常数),而 o(Ax)是比 Ax 高阶的无穷小(注:o 读作奥密克戎,希腊字母)那么称函数 f(x)在点 x 是可微的,且 AAx 称作函数在点 x 相应于因变量增量 Ay 的微分,记作dy,即 dy=AAx。函数的微分是函数增量的主要部分,且是 Ax 的线性函数,故说函数的微分是函数增量的线性主部(巧-0)。通常把自变量 x 的增量 Ax 称为自变量的微分,记作 dx,即 dx=Ax。于是函数 y=f(x)的微分又可记作 dy=f'(x)dxo 函数因变量的微分与自变量的微分之商等于该函数的导数。因此,导数也叫做微商。当自变量 X 改变为 X+以时,相应地函数值由 f(X)改变为 f(X+^X),如果存在一个与心无关的常数A,使 f(X+^X)-f(X)和 ZX 之差是△X-O 关于以的高阶无穷小量,则称 5 是 f(X)在 X 的微分,记为dy,并称 f(X)在 X 可微。一元微积分中,可微可导等价。记 A・AX=dy,则 dy=f'(X)dX。例如:d(sinX)=cosXdX。微分概念是在解决直与曲的矛盾中产生的,在微小局部可以用直线去近似替代曲线,它的直接应用就是函数的线性化。微分具有双重意义:它表示一个微小的量,因此就可以把线性函数的数值计算结果作为本来函数的数值近似值,这就是运用微分方法进行近似计算的基本思想。积分发展的动力源自实际应用中的需求。实际操作中,有时候可以用粗略的方式进行估算一些未知量,但随着科技的发展,很多时候需要知道精确的数值。要求简单几何形体的面积或体积,可以套用已知的公式。比如一个长方体状的游泳池的容积可以用长 X 宽 X 高求出。但如果游泳池是卵形、抛物型或更加不规则的形状,就需要用积分来求出容积。物理学中,常常需要知道一个物理量(比如位移)对另一个物理量(比如力)的累积效果,这时...