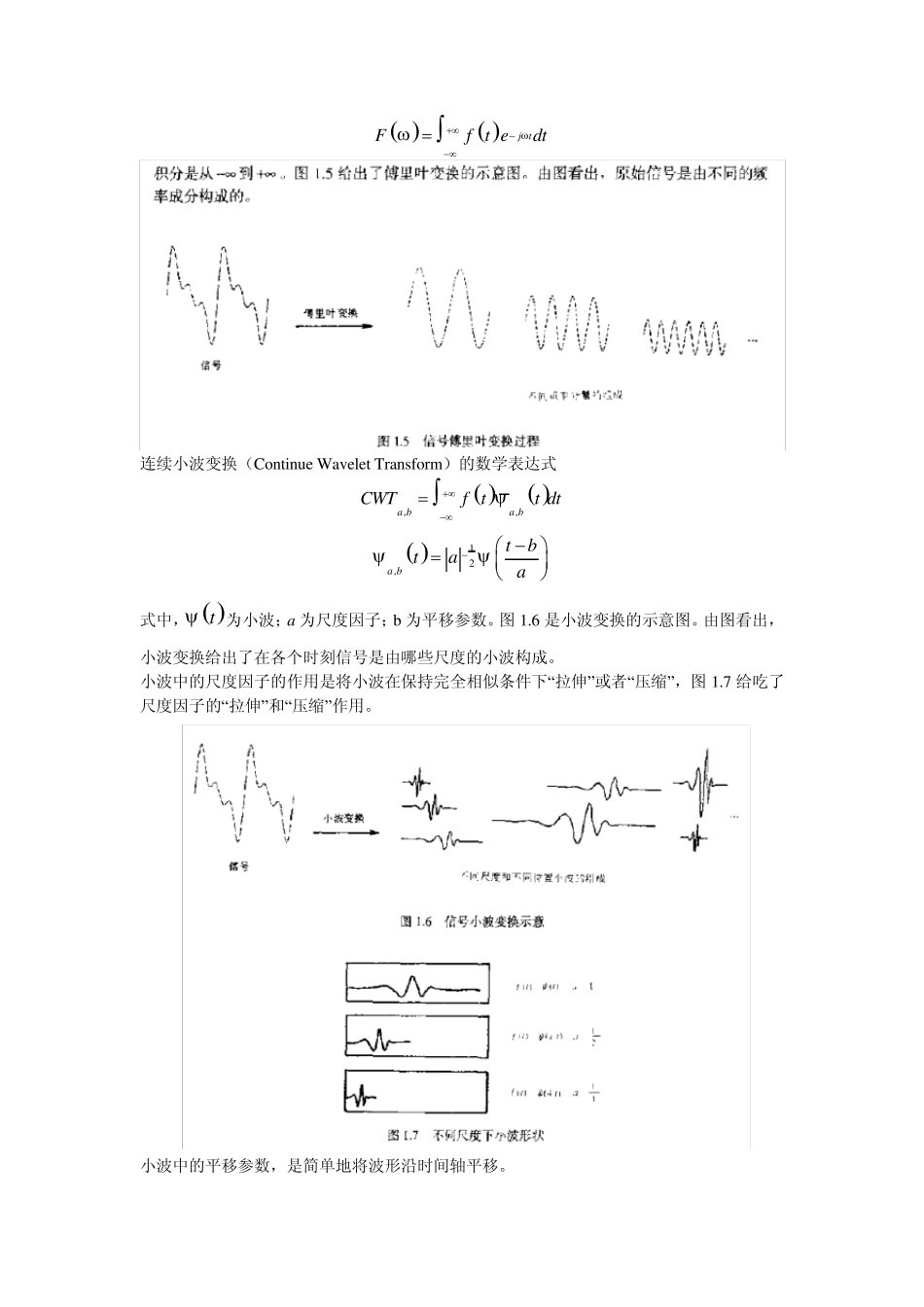
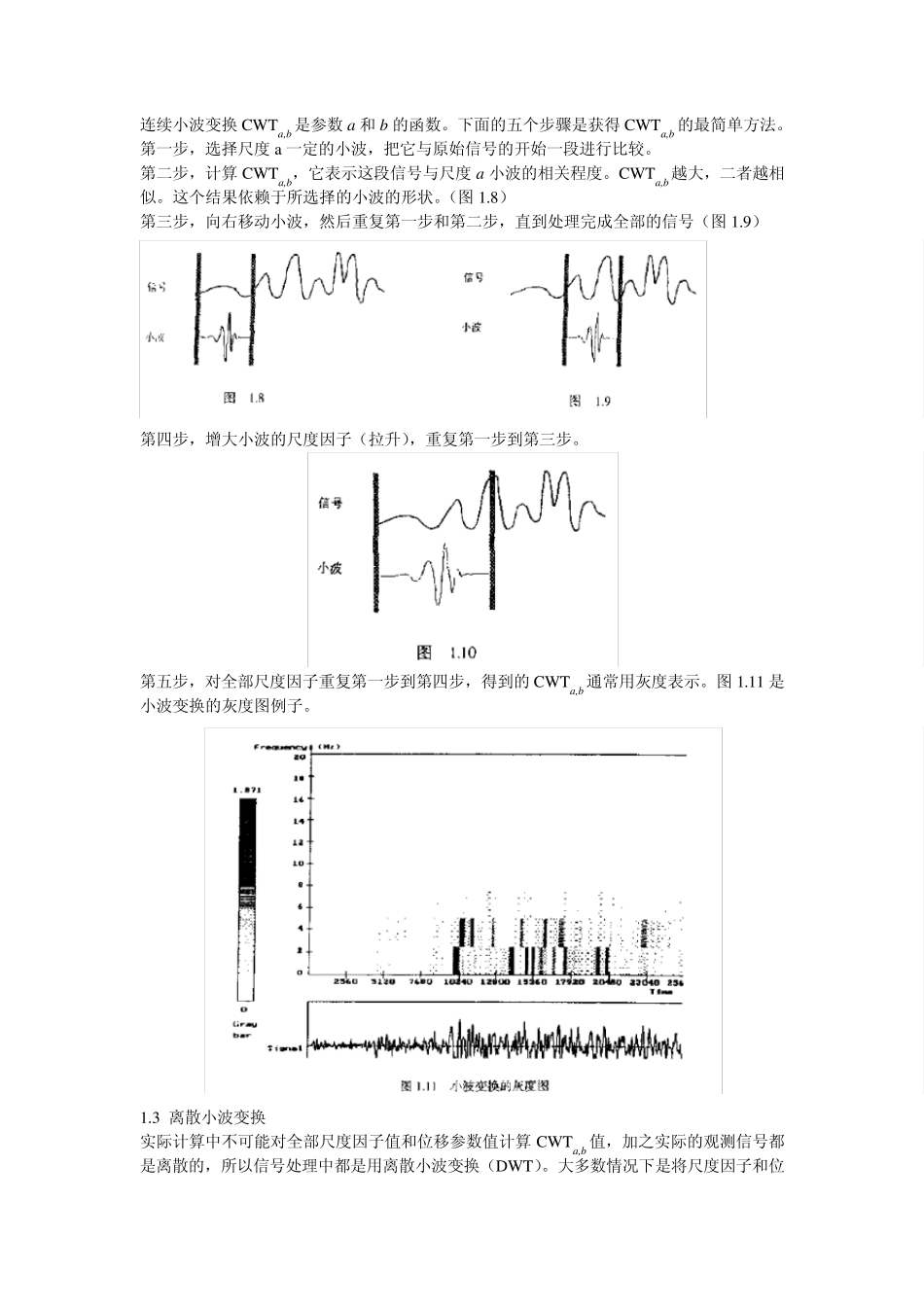
小波变换学习心得 第一章什么是小波变换 1 从傅里叶变换到小波变换 1.1 短时傅里叶变换 为了克服傅里叶变换中时域和频域不能兼容的缺点,短时傅里叶变换把一个时间信号变为时间和频率的二维函数,它能够提供信号在某个时间段和某个频率范围的一定信息。这些信息的精度依赖于时间窗的大小。短时傅里叶变换的缺点是对所有的频率成分,所取的时间窗大小相同,然而,对很多信号为了获得更精确的时间或频率信息,需要可变的时间窗。 1.2 小波变换 小波变换提出了变换的时间窗,当需要精确的低频信息时,采用长的时间窗,当需要精确的高频信息时,采用短的时间窗,图1.3 给出了时间域信号、傅里叶变换、短时傅里叶变换和小波变换的对比示意图。 由图1.3 看出,小波变换用的不是时间-频率域。而是时间-尺度域,尺度越大,采用越大的时间窗,尺度越小,采用越短的时间窗,即尺度与频率成反比。 1.2 连续小波变换 小波是一个衰减的波形,它在有限的区域里存在(不为零),且其均值为零。图1.4 是一个Daubechies 小波(db10)与正弦波的比较。 正弦波:随时间无限振动的光滑波形,小波变换:尖锐变化而且是无规则的波形。因此小波能更好的刻画信号的局部特性。 在数学上,傅里叶变换的公式为 j tFf t edt 连续小波变换(Continu e Wav elet Transform)的数学表达式 ,,a ba bCWTf tt dt 12,a bt btaa 式中, t为小波;a 为尺度因子;b 为平移参数。图 1.6 是小波变换的示意图。由图看出,小波变换给出了在各个时刻信号是由哪些尺度的小波构成。 小波中的尺度因子的作用是将小波在保持完全相似条件下“拉伸”或者“压缩”,图 1.7 给吃了尺度因子的“拉伸”和“压缩”作用。 小波中的平移参数,是简单地将波形沿时间轴平移。 连续小波变换CWTa ,b 是参数a 和b 的函数。下面的五个步骤是获得 CWTa ,b 的最简单方法。 第一步,选择尺度 a一定的小波,把它与原始信号的开始一段进行比较。 第二步,计算 CWTa ,b ,它表示这段信号与尺度 a 小波的相关程度。CWTa ,b 越大,二者越相似。这个结果依赖于所选择的小波的形状。(图 1.8) 第三步,向右移动小波,然后重复第一步和第二步,直到处理完成全部的信号(图 1.9) 第四步,增大小波的尺度因子(拉升),重复第一步到第三步。 第五步,...