微积分(曹定华)课后题答案第一章习题详解

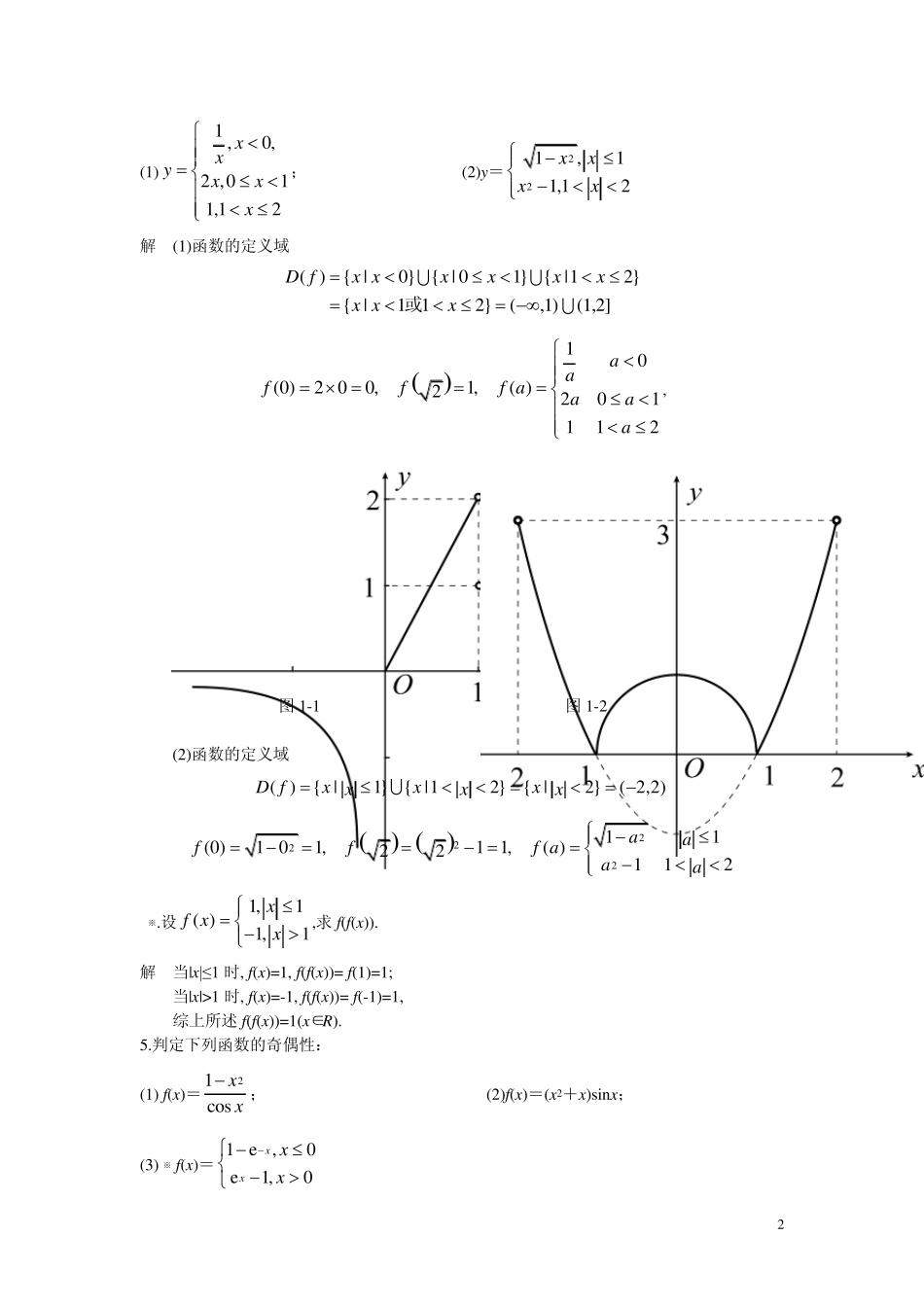
1 第一章 习题1 -1 1.用区间表示下列不等式的解 2(1)9;(2)1;1(3)(1)(2)0;(4)00.011 xxxxx 解 (1)原不等式可化为(3)(3)0xx,其解为33x ,用区间表示是[-3,3]. (2) 原不等式可化为11x  或11x   , 其解为2x 或0x , 用区间表示是(-∞,0)∪(2,+ ∞). (3)原不等式的解为21x ,用区间表示是(-2,1). (4)原不等式可化为0.0110.0110xx   即1.010.991xx   用区间表示是(-1.01,-1)∪(-1,-0.99). 2.用区间表示下列函数的定义域: 221(1)1;(2)arcsin(1)lg(lg );1(3)65.ln(2) yxyxxxyxxx 解 (1)要使函数有意义,必须2010xx 即011xx  所以函数的定义域为[-1,0)∪(0,1]. (2)要使函数有意义,必须1 11lg00xxx   即0210xxx   所以函数的定义域是12x,用区间表示就是(1,2]. (3)要使函数有意义,必须2650ln(2)020xxxx  即6112xxx    所以函数的定义域是-6≤x <1,用区间表示就是[-6,1). 3.确定下列函数的定义域及求函数值 f(0),f(2 ),f(a)(a 为实数),并作出图形 2 (1)1 ,0,2 ,011,12xxyxxx ； (2)y ＝221,11,12xxxx 解 (1)函数的定义域 ( ){ |0}{ | 01}{ |12}{ |1 12}(,1)(1,2]或D fx xxxxxx xx  10(0)2 00,1,( )2201112 aafff aaaa , 图1-1 图1-2 (2)函数的定义域 ( ){ |1}{ |12}{ |2}( 2,2)D fxxxxxx   222211(0)1 01,11,( )22112 aafff aaa   4※.设1,1( )1,1xf xx ,求 f(f(x )). 解 当|x |≤ 1 时, f(x )=1, f(f(x ))= f(1)=1; 当|x |>1 时, f(x )=-1, f(f(x ))= f(-1)=1, 综上所述 f(f(x ))=1(x ∈R). 5.判定下列函数的奇偶性： (1) f(x )＝21cosxx； (2)f(x )＝(x 2＋x )sinx ； (3) ※ f(x )＝1 e,0e1,0xxxx  3 解 (1) 221 ()1()( )cos()cosxxfxf xxx  ∴f(x )是偶函数. (2) 222()[()()]sin()()( sin )()sin( )fxx...